長野県佐久市八幡 八幡神社 安永9年(1780)
中村信弥「改訂増補 長野県の算額」県内の算額(P.34)
http://www.wasan.jp/zoho/zoho.html
キーワード:外円,正方形,矢
#Julia #SymPy #算額 #和算 #数学
円の中に正方形と 4 本の矢を容れる。矢の長さの二乗と外積(円の面積から正方形の面積を除いたもの)の和が 9.8,円の直径の平方根と円周の和が 14.8 のとき,矢の長さはいかほどか。ただし,円周率としては 3.2 を用いよ。
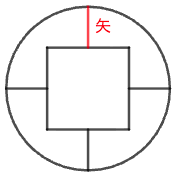
矢の長さを \(x\),円の半径を \(r\),正方形の一辺の長さを \(s\) とおき,以下の連立方程式を解く。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms x, r, s, 円周率, A, B
s = 2r - 2x
eq1 = x^2 + 円周率*r^2 - s^2 - A
eq2 = sqrt(2r) + 円周率*2r - B;
まず,eq2 を解き \(r\) を求める。
# r: 円の半径
ans_r = solve(eq2, r)[1] # 1 of 2
@show(ans_r)
ans_r = (2*B*円周率 - sqrt(4*B*円周率 + 1) + 1)/(4*円周率^2)
\(\displaystyle \frac{2 B 円周率 - \sqrt{4 B 円周率 + 1} + 1}{4 円周率^{2}}\)
eq1 の \(r\) に \(ans_r\) を代入し,得られる方程式を解いて \(x\) を求める。
eq1_2 = eq1(r => ans_r)
\(\displaystyle - A + x^{2} - \left(- 2 x + \frac{2 B 円周率 - \sqrt{4 B 円周率 + 1} + 1}{2 円周率^{2}}\right)^{2} + \frac{\left(2 B 円周率 - \sqrt{4 B 円周率 + 1} + 1\right)^{2}}{16 円周率^{3}}\)
# x: 矢の長さ
ans_x = solve(eq1_2, x)[1]
@show(ans_x)
ans_x = (2*B*円周率/3 - sqrt(4*B*円周率 + 1)/3 - sqrt(-48*A*円周率^4 + 12*B^2*円周率^3 + 16*B^2*円周率^2 - 12*B*円周率^2*sqrt(4*B*円周率 + 1) + 24*B*円周率^2 - 16*B*円周率*sqrt(4*B*円周率 + 1) + 32*B*円周率 - 6*円周率*sqrt(4*B*円周率 + 1) + 6*円周率 - 8*sqrt(4*B*円周率 + 1) + 8)/12 + 1/3)/円周率^2
\(\displaystyle \frac{\frac{2 B 円周率}{3} - \frac{\sqrt{4 B 円周率 + 1}}{3} - \frac{\sqrt{- 48 A 円周率^{4} + 12 B^{2} 円周率^{3} + 16 B^{2} 円周率^{2} - 12 B 円周率^{2} \sqrt{4 B 円周率 + 1} + 24 B 円周率^{2} - 16 B 円周率 \sqrt{4 B 円周率 + 1} + 32 B 円周率 - 6 円周率 \sqrt{4 B 円周率 + 1} + 6 円周率 - 8 \sqrt{4 B 円周率 + 1} + 8}}{12} + \frac{1}{3}}{円周率^{2}}\)
A = 9.8, B = 14.8, 円周率 = 3.2 のとき,矢の長さは 1 である。
ans_x(A => 98//10, B => 148//10, 円周率 => 32//10)
\(1\)
ちなみに,円周率として \(\pi = 3.141592653589793\) を用いたとき,A = 103, B = 50 のとき,矢の長さは 3.00000542000365 になる。ただし,円の直径はきれいな数ではない。
ans_x(A => 103, B => 50, 円周率 => 3.141592653589793)
\(3.00000542000365\)
ans_r(A => 103, B => 50, 円周率 => 3.141592653589793)
\(7.3476360257415\)
以下のアイコンをクリックして応援してください