43 岩手県一関市滝沢字寺田下 熊野白山滝神社 明治13年(1880)
安富有恒:和算—岩手の現存算額のすべて,青磁社,東京都,1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード:直角三角形,正方形,斜線
#Julia #SymPy #算額 #和算 #数学
全円の中に 2 本の斜線 \({\rm AC},\ {\rm AD}\) と 2 個の正方形を容れる。片方の斜線 \({\rm AC}\) は円周上にある 2 頂点を結ぶもの,もう一方の斜線 \({\rm AD}\) は片方の正方形の一辺 \({\rm AB}\) を延長したもので,もう片方の正方形の円周上の頂点 \({\rm D}\) を結ぶものである。全円の直径が与えられたとき,赤く色付けした弓形の面積はいかほどか。
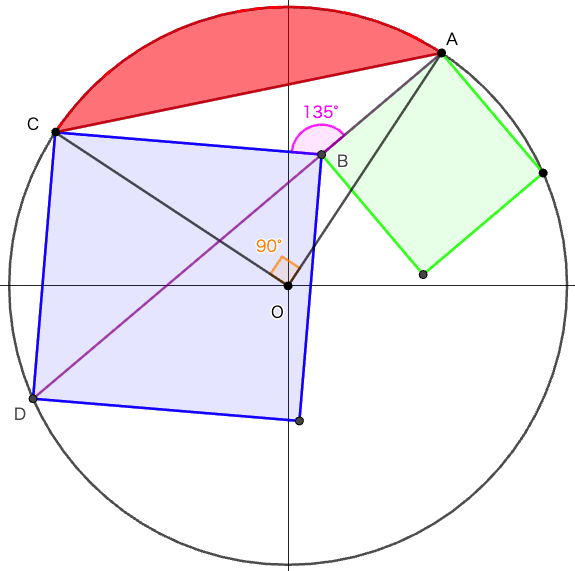
ややこしそうに書いたが,このような図は 1 種類しか描けない。描かれる図においては,必ず (1) ∠ABC = 135°,(2) ∠AOC = 90° となる。この図形については「算額(その1994)」が 参考になる。
円の半径を \(r\) とすれば,赤く色付けした部分の面積は,円の面積の 1/4 から,直角二等辺三角形 ABC の面積を除いた面積である。
\(\displaystyle \displaystyle \frac{\pi r^2}{4} - \frac{r^2}{2} = \frac{r^2(\pi - 2)}{4}\)
using SymPy
@syms r
S = PI*r^2/4 - r^2/2 |> factor
\(\displaystyle \frac{r^{2} \left(-2 + \pi\right)}{4}\)
円の直径が 1 のとき,赤く色付けした部分の面積は 0.0713495408493621 である。
S(r => 1/2).evalf()
\(0.0713495408493621\)
術は,「置円責率内減五分余四乗全円巾」つまり「円周率の 1/4 から 0.5 を引いて,直径の二乗を掛ける」なので,同じ式である。
円積率 = PI/4
S = (円積率 - 1//2)/4*(2r)^2
\(\displaystyle 4 r^{2} \left(- \frac{1}{8} + \frac{\pi}{16}\right)\)
S |> simplify
\(\displaystyle \frac{r^{2} \left(-2 + \pi\right)}{4}\)
S(r => 1/2).evalf()
\(0.0713495408493621\)
以下のアイコンをクリックして応援してください