算額（その1789） - 算額あれこれ

岐阜県大垣市西外側町大垣八幡神社（大垣八幡宮）天保年間

http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF
キーワード：円2個，半円，台形
#Julia #SymPy #算額 #和算 #数学

半梯の中に，半円 1 個（黄円），円 2 個（赤円，黒円）を容れる。赤円と黒円の直径を知って，黄円の直径を求めよ。

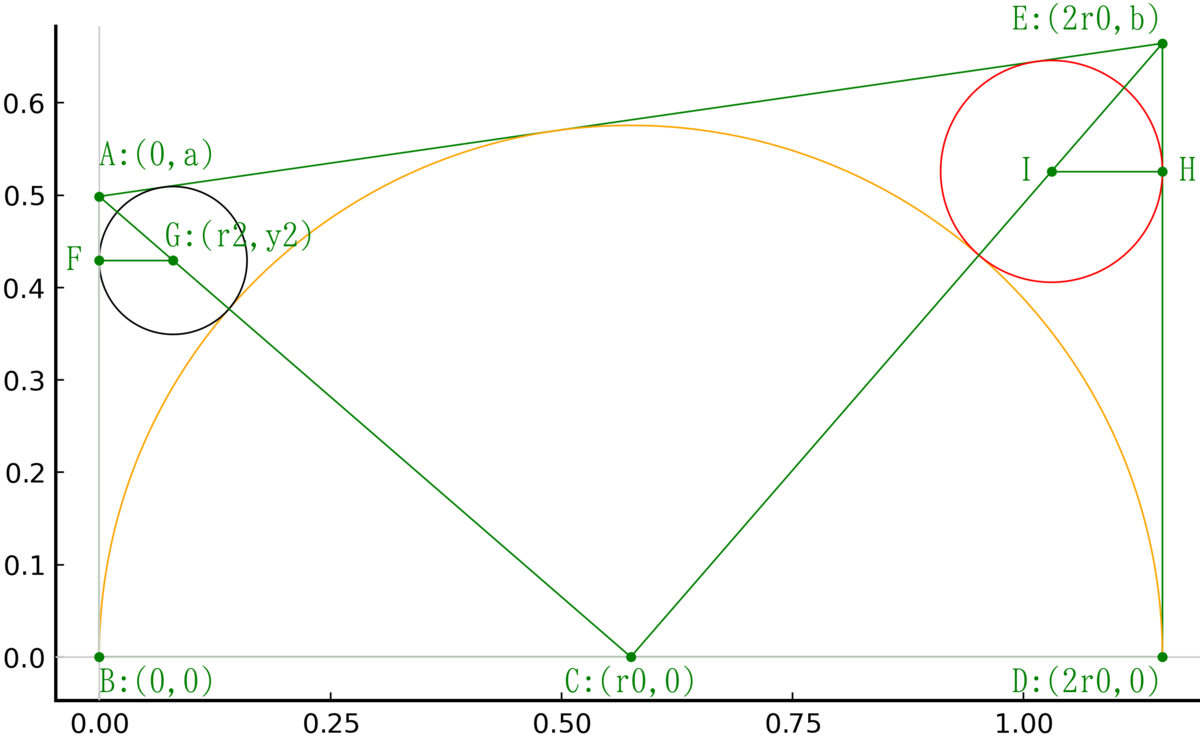
注：半梯とは，等脚台形を上底と下底の中点を結ぶ線で二等分した片方の台形である。

半梯の上底と下底を \(a,\ b\)
黄円の半径と中心座標を \(r_0,\ (r_0,\ 0)\)
赤円の半径と中心座標を \(r_1,\ (2r_0 - r_1,\ y_1);\ y_1 =\sqrt{r_0\ r_1}\)
黒円の半径と中心座標を \(r_2,\ (r_2,\ y_2);\ y_2 =\sqrt{r_0\ r_2}\)
とおく。

まず，既知の \(r_1,\ r_2\) から \(r_0\) を求める。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms r0::positive, r1::positive, y1::positive, r2::positive, y2::positive, a::positive, b::positive

# ⊿ABC ∽ ⊿CDE なので AB/BC = CD/DE/b
eq1 = a/r0 - r0/b
# ⊿ABC において
# AC = sqrt(AB^2 + BC^2)
# ⊿AFG ∽ ⊿ABC なので AG/FG = AC/BC
# AC = AG + GC
eq2 = r2*sqrt(a^2 + r0^2)/r0 + r2 + r0 - sqrt(a^2 + r0^2)
# ⊿CDE において，同様にして
eq3 = r1*sqrt(b^2 + r0^2)/r0 + r1 + r0 - sqrt(b^2 + r0^2);

eq2 から \(a\) を求める。

ans_a = solve(eq2, a)[2] # 2 0f 2

　\(\displaystyle \frac{2 r_{0}^{\frac{3}{2}} \sqrt{r_{2}}}{\left|{r_{0} - r_{2}}\right|}\)

\( (r_0 > r_2)\) なので，\(\text{Abs}()\) を外す。

ans_a = ans_a |> numerator |> x -> x/(r0 - r2)

　\(\displaystyle \frac{2 r_{0}^{\frac{3}{2}} \sqrt{r_{2}}}{r_{0} - r_{2}}\)

eq3 から \(b\) を求める。

ans_b = solve(eq3, b)[2]# # 2 0f 2

　\(\displaystyle \frac{2 r_{0}^{\frac{3}{2}} \sqrt{r_{1}}}{\left|{r_{0} - r_{1}}\right|}\)

\( (r_0 > r_1)\) なので，\(\text{Abs}()\) を外す。

ans_b = ans_b |> numerator |> x -> x/(r0 - r1)

　\(\displaystyle \frac{2 r_{0}^{\frac{3}{2}} \sqrt{r_{1}}}{r_{0} - r_{1}}\)

eq1 に \(ans_a,\ ans_b\) を代入し，\(r_0\) について解く。

eq0 = eq1(a => ans_a, b => ans_b)

　\(\displaystyle \frac{2 \sqrt{r_{0}} \sqrt{r_{2}}}{r_{0} - r_{2}} - \frac{r_{0} - r_{1}}{2 \sqrt{r_{0}} \sqrt{r_{1}}}\)

res = solve(eq0, r0)[2] # 2 of 2

　\(\displaystyle 2 \sqrt{r_{1}} \sqrt{r_{2}} + \frac{r_{1}}{2} + \frac{r_{2}}{2} + \frac{\sqrt{8 r_{1}^{\frac{3}{2}} \sqrt{r_{2}} + 8 \sqrt{r_{1}} r_{2}^{\frac{3}{2}} + r_{1}^{2} + 14 r_{1} r_{2} + r_{2}^{2}}}{2}\)

この式でも十分であるが，以下のように進める。
ルートの中身 res.args[3] について \(\sqrt{r_1}\) を \(s\)，\(\sqrt{r_2}\) を \(t\) と置き換え，2 乗し，因数分解し，再度 \(s\) を\( \sqrt{r_1}\), \(t\) を \(\sqrt{r_2}\) に戻す。

@syms s, t
temp = res.args[3](√r1 => s, √r2 => t)^2 |> factor |> x -> x(s => √r1, t => √r2)

　\(\displaystyle \frac{\left(\sqrt{r_{1}} + \sqrt{r_{2}}\right)^{2} \left(6 \sqrt{r_{1}} \sqrt{r_{2}} + r_{1} + r_{2}\right)}{4}\)

\(r_0\) を求める式は，以下のようになる。

ans_r0 = res.args[1] + res.args[2] + sqrt(temp) + res.args[4]

　\(\displaystyle 2 \sqrt{r_{1}} \sqrt{r_{2}} + \frac{r_{1}}{2} + \frac{r_{2}}{2} + \frac{\left(\sqrt{r_{1}} + \sqrt{r_{2}}\right) \sqrt{6 \sqrt{r_{1}} \sqrt{r_{2}} + r_{1} + r_{2}}}{2}\)

ans_r0 |> println

2*sqrt(r1)*sqrt(r2) + r1/2 + r2/2 + (sqrt(r1) + sqrt(r2))*sqrt(6*sqrt(r1)*sqrt(r2) + r1 + r2)/2

たとえば，赤円，黒円の半径が　\(r_1 = 0.12,\ r_2 => 0.08\) のとき，黄円の半径は \(r_0 = 0.575229363804251\) となる。

ans_r0(r1 => 0.12, r2 => 0.08) |> println

0.575229363804251

術に基づき，赤径，黒径を与えて黄径を得る関数は以下のように定義することができ，たとえば赤径が 0.24，黒径が 0.16 のとき，黄径は 1.1504587276085014（半径は 0.5752293638042507 となり，前述の解と一致する。

function 黄径(赤径, 黒径)
天 = 赤径*黒径
地 = (赤径 + 黒径)/2 + 2√天
地 + sqrt(地^2 - 天)
end;
黄径(2*0.12, 2*0.08) |> println
黄径(2*0.12, 2*0.08)/2 |> println

1.1504587276085014
0.5752293638042507

\(r_0\) が求まれば，後退代入により \(a,\ b\) が求まる。

ans_a |> println

2*r0^(3/2)*sqrt(r2)/(r0 - r2)

ans_b |> println

2*r0^(3/2)*sqrt(r1)/(r0 - r1)

また，赤円，黒円の中心の \(y\) 座標は \(\sqrt{r_0\ r_1},\ \sqrt{r_0\ r_2}\) である。

\(r_1 = 0.12,\ r_2 => 0.08\) のとき，すべてのパラメータは以下の通りである。

\(r_0 = 0.575229,\ a = 0.498345,\ b = 0.663975,\ y_1 = 0.525462,\ y_2 = 0.429038\)

描画関数プログラムのソースを見る

function draw(r1, r2, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho", dpi=500)
r0 = 2√(r1*r2) + r1/2 + r2/2 + (√r1 + √r2)*sqrt(6√(r1*r2) + r1 + r2)/2
a = 2r0^(3/2)*√r2/(r0 - r2)
b = 2r0^(3/2)*√r1/(r0 - r1)
y1 = 2sqrt(r0*r1)
y2 = 2sqrt(r0*r2)
@printf("r1 = %g, r2 = %g, r0 = %g, a = %g, b = %g, y1 = %g, y2 = %g\n", r1, r2, r0, a, b, y1, y2)
plot([0, 2r0, 2r0, 0, 0], [0, 0, b, a, 0], color=:green, lw=0.5)
circle(r0, 0, r0, beginangle=0, endangle=180)
circle(2r0 - r1, y1, r1, :magenta)
circle(r2, y2, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, a, "A:(0,a)", :green, :left, :bottom, delta=3delta)
point(0, 0, "B:(0,0)", :green, :left, delta=-delta)
point(r0, 0, "C:(r0,0)", :green, :center, delta=-delta)
point(2r0, 0, "D:(2r0,0)", :green, :right, delta=-delta)
point(2r0, b, "E:(2r0,b)", :green, :right, :bottom, delta=delta)
plot!([0, r0, 2r0], [a, 0, b], color=:green, lw=0.5)
point(0, y2, "F ", :green, :right, :vcenter)
point(r2, y2, "G:(r2,y2)", :green, :left, :bottom, delta=delta, deltax=-delta)
segment(0, y2, r2, y2, :green)
point(2r0, y1, " H", :green, :left, :vcenter)
point(2r0 - r1, y1, "I ", :green, :right, :vcenter)
segment(2r0 - r1, y1, 2r0, y1, :green)
plot!(xlims=(-5delta, 2r0 + 2delta), ylims=(-5delta, b + 2delta))
end
end;