『容術新題』(鈴木円著)其六
深川英俊,ダン・ペドー:日本の幾何—何題解けますか,森北出版株式会社,1991.
キーワード:円3個,四分円,正方形,斜線
#Julia #SymPy #算額 #和算 #数学
一辺の長さが \(a\) の正方形内に,直線,円,円弧などを設けるとき,小円の半径は,100 個の問題について全く同じ答 \(a/16\) になることを示せ。
其六:正方形の中に,四分円 1 個,斜線 1 本を設け,大円 1 個,小円 2 個を容れる。
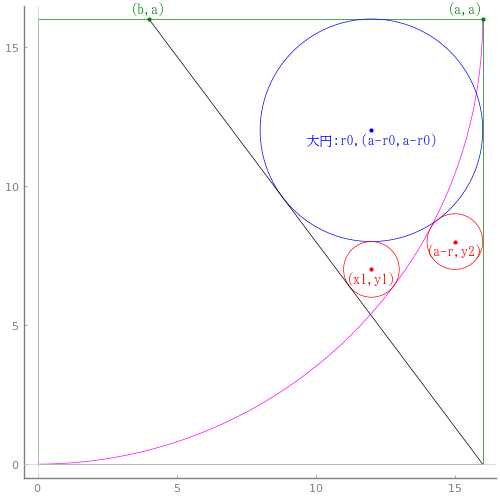
正方形の一辺の長さを \(a\)
斜線と正方形の一辺との交点座標を \( (b, a)\)
大円の半径と中心座標を \(r_0, (a - r_0, a - r_0)\)
小円の半径と中心座標を \(r, (x_1, y_1), (a - r, y_2)\)
とおき,以下の連立方程式を解く。
途中の式が複雑になるので \(a = 16\) として,一般性を失わない。
なお,大円と左側の小円の中心の \(x\) 座標は等しいものと仮定して解く(結果としてその仮定は正しいことがわかった)。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms r::positive, a::positive, b::positive, r0::positive, x1::positive, y1::positive, y2::positive
a = 16
x1 = a - r0
eq1 = (a - r)^2 + (a - y2)^2 - (a + r)^2
eq2 = (r0 - r)^2 + (a - r0 - y2)^2 - (r0 + r)^2
eq3 = (x1 - (a - r0))^2 + (a - r0 - y1)^2 - (r0 + r)^2
eq4 = dist2(b, a, a, 0, a - r0, a - r0, r0)
eq5 = dist2(b, a, a, 0, x1, y1, r);
まず,eq1 から \(y_2\) を求める。
ans_y2 = solve(eq1, y2)[1]
\(\displaystyle 16 - 8 \sqrt{r}\)
eq2, eq3 に代入し,連立方程式を解いて \(y_1, r_0\) を求める。
eq2 = eq2(y2 => ans_y2) |> expand |> simplify
\(\displaystyle - 16 \sqrt{r} r_{0} - 4 r r_{0} + 64 r + r_{0}^{2}\)
eq3 = eq3 |> expand |> simplify
\(\displaystyle - r^{2} - 2 r r_{0} + 2 r_{0} y_{1} - 32 r_{0} + y_{1}^{2} - 32 y_{1} + 256\)
(ans_y1, ans_r0) = solve([eq2, eq3], (y1, r0))[2] # 2 of 4
(-16*sqrt(r) - 5*r + 4*sqrt(8*r^(3/2) + r^2) + 16, 8*sqrt(r) + 2*r - 2*sqrt(8*r^(3/2) + r^2))
eq4 に \(r_0\) を代入し \(b\) を求める。
eq4 = eq4(r0 => ans_r0)|> expand |> simplify
\(\displaystyle - 256 b^{2} \sqrt{r} - 64 b^{2} r + 64 b^{2} \sqrt{8 r^{\frac{3}{2}} + r^{2}} + 256 b^{2} - 2048 b r^{\frac{3}{2}} + 1024 b \sqrt{r} \sqrt{8 r^{\frac{3}{2}} + r^{2}} + 12288 b \sqrt{r} - 256 b r^{2} + 256 b r \sqrt{8 r^{\frac{3}{2}} + r^{2}} + 1024 b r - 3072 b \sqrt{8 r^{\frac{3}{2}} + r^{2}} - 8192 b + 32768 r^{\frac{3}{2}} - 16384 \sqrt{r} \sqrt{8 r^{\frac{3}{2}} + r^{2}} - 131072 \sqrt{r} + 4096 r^{2} - 4096 r \sqrt{8 r^{\frac{3}{2}} + r^{2}} + 32768 \sqrt{8 r^{\frac{3}{2}} + r^{2}} + 65536\)
ans_b = solve(eq4, b)[2] # 2 of 2
\(\displaystyle \frac{4 \left(- 8 r^{\frac{3}{2}} + 4 \sqrt{r} \sqrt{8 r^{\frac{3}{2}} + r^{2}} + 32 \sqrt{r} - r^{2} + r \sqrt{8 r^{\frac{3}{2}} + r^{2}} - 8 \sqrt{8 r^{\frac{3}{2}} + r^{2}} - 16\right)}{4 \sqrt{r} + r - \sqrt{8 r^{\frac{3}{2}} + r^{2}} - 4}\)
最後に,eq5 に \(y1, r0, b\) を代入する。\(\sqrt{r}\) を含む式になり SymPy では解けないので,\(t = \sqrt{r}\) で変数変換した式を解く。
@syms t
eq5 = eq5(y1 => ans_y1, r0 => ans_r0)(b => ans_b)(sqrt(r) => t) |> simplify |> numerator
\(\displaystyle 256 t \left(5 t^{11} + 116 t^{10} - 5 t^{9} \sqrt{t^{3} \left(t + 8\right)} + 964 t^{9} - 96 t^{8} \sqrt{t^{3} \left(t + 8\right)} + 3216 t^{8} - 620 t^{7} \sqrt{t^{3} \left(t + 8\right)} + 2115 t^{7} - 1344 t^{6} \sqrt{t^{3} \left(t + 8\right)} - 7384 t^{6} + 573 t^{5} \sqrt{t^{3} \left(t + 8\right)} - 4292 t^{5} + 3300 t^{4} \sqrt{t^{3} \left(t + 8\right)} + 8912 t^{4} - 1380 t^{3} \sqrt{t^{3} \left(t + 8\right)} - 1608 t^{3} - 1984 t^{2} \sqrt{t^{3} \left(t + 8\right)} - 1536 t^{2} + 1472 t \sqrt{t^{3} \left(t + 8\right)} + 512 t - 256 \sqrt{t^{3} \left(t + 8\right)}\right)\)
小円の半径は 1 となり,小円の半径は \(a/16\) である。
ans_r = solve(eq5, t)[2]^2 # 2 of 4
\(\displaystyle 1\)
他のパラメータは後退代入によって求まる。
ans_b(r => 1)
\(\displaystyle 4\)
ans_y2(r => 1)
\(\displaystyle 8\)
ans_y1(r => 1)
\(\displaystyle 7\)
ans_r0(r => 1)
\(\displaystyle 4\)
描画関数プログラムのソースを見る
function draw(a, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho",
fg_color_border=:gray50, fg_color_text=:gray50, fg_color_axis=:gray50)
a=16
(r, b, r0, y1, y2) = [1, 4, 4, 7, 8]
x1 = a - r0
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
circle(0, a, a, :magenta, beginangle=270, endangle=360)
circle(a - r0, a - r0, r0, :blue)
circle(x1, y1, r)
circle(a - r, y2, r)
segment(b, a, a, 0)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a, a, "(a,a)", :green, :right, :bottom, delta=delta/2)
point(b, a, "(b,a)", :green, :center, :bottom, delta=delta/2)
point(a - r0, a - r0, "大円:r0,(a-r0,a-r0)", :blue, :center, delta=-delta/2)
point(x1, y1, "(x1,y1)", :red, :center, delta=-delta/2)
point(a - r, y2, "(a-r,y2)", :red, :center, delta=-delta/2)
end
end;
draw(16, true)
以下のアイコンをクリックして応援してください