45 岩手県一関市舞川字龍ヶ沢 観福寺観音堂 明治34年(1901)
安富有恒:和算—岩手の現存算額のすべて,青磁社,東京都,1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード:円4個,四分円,菱形
#Julia #SymPy #算額 #和算 #数学
菱形の中に四分円 2 個を設け,大小円を 2 小ずつ容れる。小円の直径が与えられたとき,大円の直径はいかほどか。
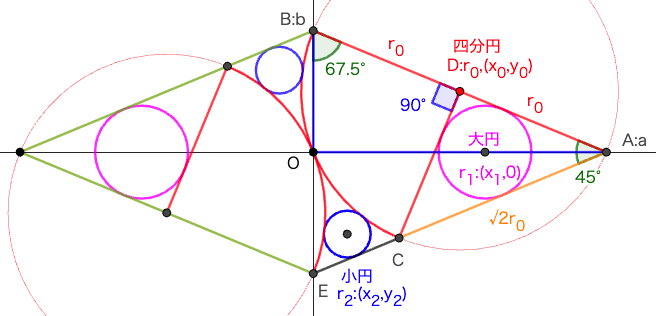
図形の対称性から,四分円は原点を通る。また,菱形に内接する四分円は \({\rm ∠BCD = 90°}\) なので,右上の菱形の一辺 \({\rm AB}\) を直径とする円の 1/4 である。したがって,大円は二等辺三角形 \({\rm ACD}\) に内接するので,大円の半径は簡単に求めることができる。
また,\(∠ABO = 67.5°,\ ∠BAO = 22.5°\) である。
小円の半径は小円の中心と右下のひし形の一辺 \({\rm AE}\) までの距離が半径に等しいという条件で決まる。
菱形の対角線を \(a,\ b,\ a >b\)
四分円の半径と中心座標を \(r_0,\ (x_0,\ 0)\)
大円の半径と中心座標を \(r_1,\ (\sqrt{2}b,\ 0)\)
小円の半径と中心座標を \(r_2,\ (x_2,\ y_2)\)
とおき,以下のように計算を進める。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a::positive, b::positive, r0::positive, x0::positive, y0::positive,
r1::positive, x1::positive, y1, r2::positive, x2::positive, y2::negative
# b: 短い方の対角線の半分
# b = 1
# a: 長い方の対角線の半分
θ675 = Sym(675)//10 # 67.5°
a = b*tand(θ675)
@show(a)
a = b*(1 + sqrt(2))
\(b \left(1 + \sqrt{2}\right)\)
a(b => 1).evalf()
\(2.41421356237309\)
# r0: 四分円の半径
r0 = sqrt(a^2 + b^2)/2 |> simplify
@show(r0)
r0 = b*sqrt(2*sqrt(2) + 4)/2
\(\displaystyle \frac{b \sqrt{2 \sqrt{2} + 4}}{2}\)
r0(b => 1).evalf()
\(1.30656296487638\)
# 四分円の中心の x 座標
θ = Sym(225)//10
x0 = r0*cosd(θ) # simplify しない
@show(x0 |> simplify)
x0 |> simplify = b*sqrt(2*sqrt(2) + 3)/2
\(\displaystyle \frac{b \sqrt{2 \sqrt{2} + 3}}{2}\)
x0.evalf()
\(1.20710678118655 b\)
# 四分円の中心の y 座標
y0 = r0*sind(θ) # simplify しない
@show(y0 |> simplify)
y0 |> simplify = b/2
\(\displaystyle \frac{b}{2}\)
y0(b => 1).evalf()
\(0.5\)
## 大円の半径と中心座標, y 座標は 0
# r1: 大円の半径
s2 = sqrt(Sym(2)) # √2
r1 = (2r0 - s2*r0)/2 |> simplify
@show(r1)
r1 = b*(-1 + sqrt(2))*sqrt(sqrt(2) + 2)/2
\(\displaystyle \frac{b \left(-1 + \sqrt{2}\right) \sqrt{\sqrt{2} + 2}}{2}\)
ans_x1 = solve(dist2(0, -b, a, 0, x1, 0, r1), x1)[2] # 2 of 2
@show(ans_x1 |> simplify)
ans_x1 |> simplify = b*(-sqrt(6 - 4*sqrt(2)) - sqrt(3 - 2*sqrt(2)) + 1 + sqrt(2))
\(b \left(- \sqrt{6 - 4 \sqrt{2}} - \sqrt{3 - 2 \sqrt{2}} + 1 + \sqrt{2}\right)\)
ans_x1 |> sympy.sqrtdenest
\(- \sqrt{2} b \left(-1 + \sqrt{2}\right) - b \left(-1 + \sqrt{2}\right) + b + \sqrt{2} b\)
ans_x1 = sqrt(Sym(2))b
\(\sqrt{2} b\)
ans_x1[1](b => 1).evalf()
\(1.4142135623731\)
\(x_1\) は SymPy では簡約化できないが,単に \(\sqrt{2}b\) になる。
## 小円の半径と中心座標
# 右の小円と右の四分円が外接する
eq1 = (x0 - x2)^2 + (y0 - y2)^2 - (r0 + r2)^2
# 右の小円と左の四分円が外接する
eq2 = (x2 + x0)^2 + (y2 + y0)^2 - (r0 + r2)^2
# 右下の小円の中心と右下の菱形の辺の距離が小円の半径に等しい
eq3 = dist2(0, -b, a, 0, x2, y2, r2)
\(\displaystyle \frac{\sqrt{2} b^{2}}{4} + \frac{b^{2}}{2} - \frac{\sqrt{2} b x_{2}}{2} + \frac{\sqrt{2} b y_{2}}{2} + b y_{2} - r_{2}^{2} - \frac{\sqrt{2} x_{2}^{2}}{4} + \frac{x_{2}^{2}}{2} - \frac{\sqrt{2} x_{2} y_{2}}{2} + \frac{\sqrt{2} y_{2}^{2}}{4} + \frac{y_{2}^{2}}{2}\)
res = solve([eq1, eq2], (x2, y2))[1]
(sqrt(r2)*(-1 + sqrt(2))*sqrt(2*b*sqrt(sqrt(2) + 2) + 2*sqrt(2)*b*sqrt(sqrt(2) + 2) + sqrt(2)*r2 + 2*r2)/2, -sqrt(r2)*sqrt(2*b*sqrt(sqrt(2) + 2) + 2*sqrt(2)*b*sqrt(sqrt(2) + 2) + sqrt(2)*r2 + 2*r2)/2)
# x2: 小円の中心の x 座標
ans_x2 = res[1]
@show(ans_x2)
ans_x2 = sqrt(r2)*(-1 + sqrt(2))*sqrt(2*b*sqrt(sqrt(2) + 2) + 2*sqrt(2)*b*sqrt(sqrt(2) + 2) + sqrt(2)*r2 + 2*r2)/2
\(\displaystyle \frac{\sqrt{r_{2}} \left(-1 + \sqrt{2}\right) \sqrt{2 b \sqrt{\sqrt{2} + 2} + 2 \sqrt{2} b \sqrt{\sqrt{2} + 2} + \sqrt{2} r_{2} + 2 r_{2}}}{2}\)
# y2: 小円の中心の y 座標
ans_y2 = res[2]
@show(ans_y2)
ans_y2 = -sqrt(r2)*sqrt(2*b*sqrt(sqrt(2) + 2) + 2*sqrt(2)*b*sqrt(sqrt(2) + 2) + sqrt(2)*r2 + 2*r2)/2
\(\displaystyle - \frac{\sqrt{r_{2}} \sqrt{2 b \sqrt{\sqrt{2} + 2} + 2 \sqrt{2} b \sqrt{\sqrt{2} + 2} + \sqrt{2} r_{2} + 2 r_{2}}}{2}\)
# 方程式の更新
eq3_2 = eq3(x2 => res[1], y2 => res[2]) |> numerator |> simplify
\(\displaystyle \frac{b \left(\sqrt{2} b + 2 b - 4 \sqrt{r_{2}} \sqrt{2 b \sqrt{\sqrt{2} + 2} + 2 \sqrt{2} b \sqrt{\sqrt{2} + 2} + \sqrt{2} r_{2} + 2 r_{2}} + 4 r_{2} \sqrt{2 \sqrt{2} + 4}\right)}{4}\)
# r2: 小円の半径
ans_r2 = solve(eq3_2, r2)[2] |> sympy.sqrtdenest |> simplify # 2 of 2
@show(ans_r2)
ans_r2 = sqrt(2)*b/(4*sqrt(sqrt(2) + 2))
\(\displaystyle \frac{\sqrt{2} b}{4 \sqrt{\sqrt{2} + 2}}\)
ans_r2(b => 1).evalf()
\(0.191341716182545\)
# 大円の半径は小円の半径の何倍か?
(r1/ans_r2)
\(\sqrt{2} \left(-1 + \sqrt{2}\right) \left(\sqrt{2} + 2\right)\)
(r1/ans_r2).evalf()
\(2.0\)
大円の半径は,小円の半径の 2 倍である。
# r2 が決まると x2 も決まる
ans_x2(r2 => ans_r2)(b => 1).evalf()
\(0.280330085889911\)
# r2 が決まると y2 も決まる
ans_y2(r2 => ans_r2)(b => 1).evalf()
\(-0.676776695296637\)
(sqrt(2*√Sym(2) + 4)/2).evalf()
\(1.30656296487638\)
√2(sqrt(√Sym(2) + 2)/2).evalf()
\(1.30656296487638\)
sqrt(2√2 + 4)/2
1.3065629648763766
t = sqrt(√2 + 2)
√2t/2
1.3065629648763766
t/√2
1.3065629648763764
描画関数プログラムのソースを見る
function draw(b, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
a = b*(1 + √2)
t = sqrt(√2 + 2)
r0 = b*t/√2
x0 = b*sqrt(2√2 + 3)/2
y0 = b/2
r2 = √2b/4t
u = sqrt(2b*t + 2√2b*t + √2r2 + 2r2)/2
x2 = sqrt(r2)*(√2 - 1)*u
y2 = -sqrt(r2)*u
v = sqrt(r2)*u
x2 = v*(√2 - 1)
y2 = -v
r1 = b*(√2 - 1)*t/2
x1 = √2b
y1 = 0
(x01, y01, x02, y02) = float.(intersection2(r0, x0, y0, 0, b, b*tand(22.5), 0))
plot([a, 0, -a, 0, a], [0, b, 0, -b, 0], color=:green, lw=0.5)
circle(x0, y0, r0, :pink, lw=0.3)
circle(x0, y0, r0, beginangle=atand(b - y0, -x0), endangle=360-atand(y0 - y01, x01 - x0))
segment(x0, y0, x01, y01, :red)
circle(-x0, -y0, r0, :pink, lw=0.3)
circle(-x0, -y0, r0, beginangle=atand(y0 - b, x0), endangle=atand(y0 - y01, x0 - x01))
segment(-x0, -y0, -x01, -y01, :red)
segment(0, b, x0, y0, :red)
@printf("r1 = %.15g, r2 = %.15g, r1/r2 = %g\n", r1, r2, r1/r2)
circle2(x1, y1, r1, :magenta)
circle(x2, y2, r2, :blue)
circle(-x2, -y2, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x0, y0, "四分円:r0,(x0,y0)", :red, :left, :bottom, delta=delta, deltax=-2delta)
point(-x0, -y0)
point(x1, y1, "大円:r1,(x1,y1)", :black, :left, delta=-delta, deltax=-5delta)
point(x2, y2, "小円:r2,(x2,y2)", :black, :left, delta=-2delta, deltax=2delta)
point(-x2, -y2)
point(0, b, "b", :green, :center, :bottom, delta=delta)
point(a, 0, "a", :green, :left, :bottom, delta=delta)
point(x01, y01, "(x01,y01)", :red, :left, :bottom, delta=delta/2, deltax=delta)
end
end;
draw(1, true)
r1 = 0.38268343236509, r2 = 0.191341716182545, r1/r2 = 2
以下のアイコンをクリックして応援してください