岩手県一関市 一関八幡神社 天保9年(1838)
今有如図 03014
https://w.atwiki.jp/sangaku/pages/198.html
キーワード:円4個,外円,円弧
#Julia #SymPy #算額 #和算 #数学
外円の中に円弧を 2 個と,等円を 3 個容れる。2 個の円弧は外円と同じ半径で,外円の円周の 1 点を通る。等円の直径が 1 寸のとき,外円の直径はいかほどか。
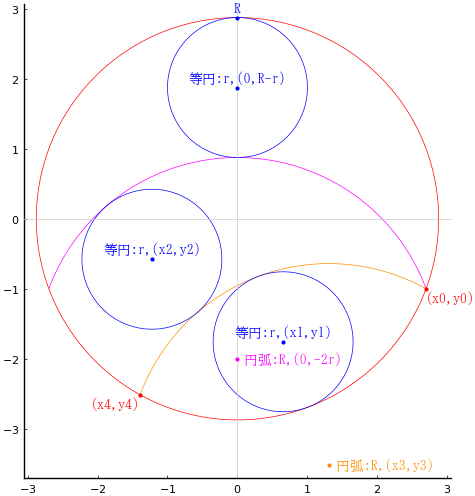
外円の半径と中心座標を \(R,\ (0,\ 0)\)
等円の半径と中心座標を \(r,\ (0,\ R - r),\ (x_1,\ y_1),\ (x_2,\ y_2)\)
円弧の半径と中心座標を \(R,\ (0,\ -2r),\ (x_3,\ y_3)\)
とおき,以下の連立方程式を解く。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms R, r, x1, y1, x2, y2, x3, y3, x0, y0
eq1 = x1^2 + y1^2 - (R - r)^2
eq2 = (x3 - x1)^2 + (y3 - y1)^2 - (R - r)^2
eq3 = (x3 - x2)^2 + (y3 - y2)^2 - (R + r)^2
eq4 = x2^2 + (y2 + 2r)^2 - (R - r)^2
eq5 = (x0 - x3)^2 + (y0 - y3)^2 - R^2
eq6 = x0^2 + (y0 + 2r)^2 - R^2
eq7 = x0^2 + y0^2 - R^2
eq8 = x1/y1 - x3/y3
eq9 = x2/(y2 + 2r) - x3/(y3 + 2r);
# solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9],
# (r, x1, y1, x2, y2, x3, y3, x0, y0))
function driver(r)
function H(u)
(R, x1, y1, x2, y2, x3, y3, x0, y0) = u
return [
x1^2 + y1^2 - (R - r)^2, # eq1
(x3 - x1)^2 + (y3 - y1)^2 - (R - r)^2, # eq2
(x3 - x2)^2 + (y3 - y2)^2 - (R + r)^2, # eq3
x2^2 + (y2 + 2r)^2 - (R - r)^2, # eq4
(x0 - x3)^2 + (y0 - y3)^2 - R^2, # eq5
x0^2 + (y0 + 2r)^2 - R^2, # eq6
x0^2 + y0^2 - R^2, # eq7
x1/y1 - x3/y3, # eq8
x2/(y2 + 2r) - x3/(y3 + 2r), # eq9
]
end;
iniv = (r/0.5).*BigFloat[1.44, 0.34, -0.88, -0.61, -0.29, 0.65, -1.75, 1.35, -0.50]
res = nls(H, ini=iniv)
res[2] && return res[1]
end;
driver(1)[1]
2.875129794162779
外円の直径は,等円の直径の 2.875129794162779 倍である。
下側の円弧と外円の交点座標 \( (x_4,\ y_4)\) は以下のようになる。
using SymPy
@syms R, r, x1, y1, x2, y2, x3, y3, x0, y0
@syms x4, y4
eq01 = (x4 - x3)^2 + (y4 - y3)^2 - R^2
eq02 = x4^2 + y4^2 - R^2
res2 = solve([eq01, eq02], (x4, y4))[1] # 1 of 2
( (x3^2 + y3^2 - 2*y3*(-x3*sqrt(-(x3^2 + y3^2)*(-4*R^2 + x3^2 + y3^2))/(2*(x3^2 + y3^2)) + y3/2))/(2*x3), -x3*sqrt(-(x3^2 + y3^2)*(-4*R^2 + x3^2 + y3^2))/(2*(x3^2 + y3^2)) + y3/2)
描画関数プログラムのソースを見る
function draw(r, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, x1, y1, x2, y2, x3, y3, x0, y0) = driver(r)
println( (R, x1, y1, x2, y2, x3, y3, x0, y0))
plot()
circle(0, 0, R)
θ = atand(y0 + 2r, x0)
circle(0, -2r, R, :magenta, beginangle=θ, endangle=180 - θ)
(x4, y4) = ( (x3^2 + y3^2 - 2*y3*(-x3*sqrt(-(x3^2 + y3^2)*(-4*R^2 + x3^2 + y3^2))/(2*(x3^2 + y3^2)) + y3/2))/(2*x3), -x3*sqrt(-(x3^2 + y3^2)*(-4*R^2 + x3^2 + y3^2))/(2*(x3^2 + y3^2)) + y3/2)
θ2 = atand(y0 - y3, x0 - x3)
θ3 = atand(y3 - y4, x3 - x4)
println(θ3)
circle(x3, y3, R, :darkorange, beginangle=θ2, endangle=180 + θ3)
circle(0, R - r, r, :blue)
circle(x1, y1, r, :blue)
circle(x2, y2, r, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R, "R", :blue, :center, :bottom, delta=delta/2)
point(0, R - r, "等円:r,(0,R-r)", :blue, :center, :bottom, delta=delta/2)
point(x1, y1, "等円:r,(x1,y1)", :blue, :center, :bottom, delta=delta/2)
point(x2, y2, "等円:r,(x2,y2)", :blue, :center, :bottom, delta=delta/2)
point(x3, y3, " 円弧:R,(x3,y3)", :darkorange, :left, :vcenter)
point(0, -2r, " 円弧:R,(0,-2r)", :magenta, :left, :vcenter)
point(x0, y0, "(x0,y0)", :red, :left, delta=-delta/2)
point(x4, y4, "(x4,y4)", :red, :right, delta=-delta/2)
end
end;
draw(1, true)
(2.875129794162779, 0.652189615220069, -1.7580558724784727, -1.22294017894271, -0.5785468478755559, 1.304379230440138, -3.5161117449569455, 2.695620769559862, -1.0)
-20.353446815337414
以下のアイコンをクリックして応援してください