二十七 群馬県太田市細谷 冠稲荷神社 文化11年(1814)
群馬県和算研究会:群馬の算額,上武印刷株式会社,高崎市,1987年3月31日.
キーワード:3次元,球,正四面体
#Julia #SymPy #算額 #和算 #数学
正四面体の中に 3 個の等球を容れる。それぞれの球は互いに外接し,正四面体の底面と側面(斜面)に接している。
正四面体の一辺の長さが 10 寸のとき,球の直径はいかほどか。
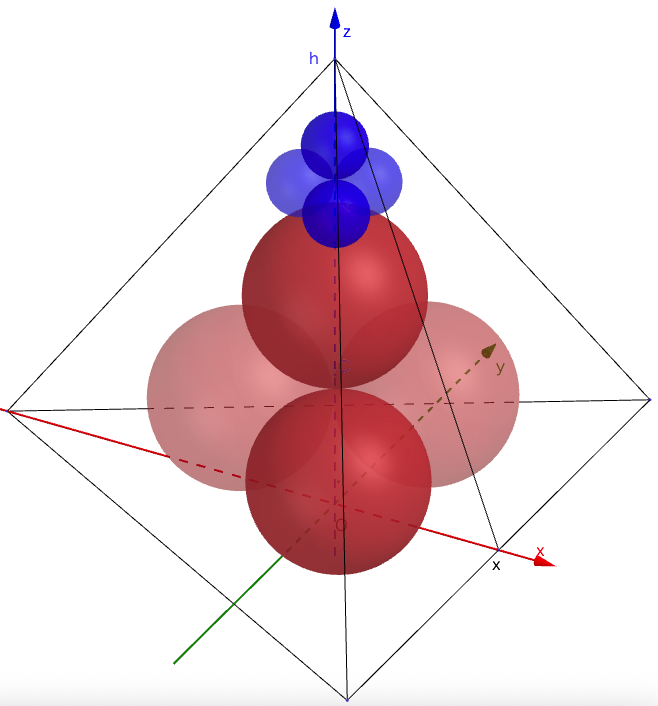
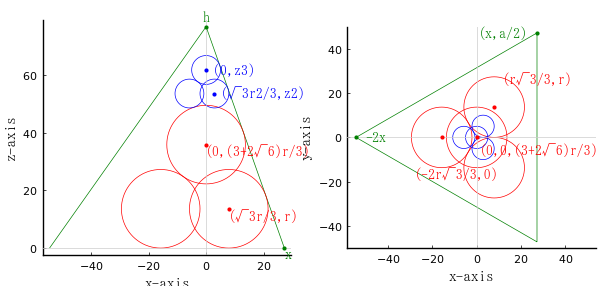
等球の半径を \(r\),正四面体の一辺の長さを \(a\) とする。
正四面体の底面の中心(重心)を原点 \(O\) とする。
正四面体の頂点の中に,大球 4 個,小球4個が入っている。一番上にある小球 1 個と大球 4 個は正四面体の 3 面に接している。下にある小球 3 個は正四面体の 2 面と他の小球と大球に接している。
大球の直径が 27.3 寸のとき,小球の直径はいかほどか。
まず,大球が正四面体に入っていることから,正四面体の一辺の長さを求める。
正四面体の高さと大球の中心座標については,大球の中心が正四面体を作ることから簡単に求めることができる。
正四面体の一辺の長さと高さを \(a, h = \sqrt{a^2 - a^2/3}\)
正四面体の底面の一辺と \(x\) 軸の交点 \(\text{X}\) の座標を \( (x,\ 0,\ 0); x = a/2\sqrt{3}\)
大球の半径と中心座標を \(r,\ (2r\sqrt{3}/3,\ r,\ r),\ (0,\ 0,\ (3 + 2\sqrt{6})r/3))\)
とおき,上にある大球の中心から,頂点と \(\text{X}\) を結ぶ線分までの距離が大球の半径に等しいという条件式 eq1 を解いて,\(a\) を求める。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a::positive, x::positive, r::positive, δ::positive, scale::positive
x = a/2√Sym(3)
h = sqrt(a^2 - a^2/3)
eq1 = dist2(0, h, x, 0, 0, (3 + 2√Sym(6))r/3, r);
eq1 を解いて \(a\) を求める。
ans_a = solve(eq1, a)[1] |> factor # 1 of 2
\(\displaystyle 2 r \left(1 + \sqrt{6}\right)\)
正四面体の一辺の長さ \(a\) は,等球の半径 \(r\) の \(2(1 + \sqrt{6})\) 倍である。
ans_a(r => 27.3/2).evalf()
\(\displaystyle 94.1710699779808\)
等球の直径が 27.3 のとき,正四面体の一辺の長さは 94.17106997798076 寸である。
\(\displaystyle a\) が既知となったので,次に,小球の半径 \(r_2\)を求める
上にある小球の中心座標を \( (0,\ 0,\ z_3)\)
下にある小球の中心座標を \( (\sqrt{3}r_2/3,\ r_2,\ z_2)\)
とおき,
上にある小球と下の小球が外接するという条件式 eq2
下にある小球と上にある大球が外接するという条件式 eq3
上にある小球の中心から,頂点と \(\text{X}\) を結ぶ線分までの距離が小球の半径に等しいという条件式 eq4
を解く。
@syms r2, z2, z3
a = 2r*(1 + √Sym(6))
x = a/2√Sym(3)
h = sqrt(a^2 - a^2/3)
eq2 = (√Sym(3)*r2/3)^2 + r2^2 + (z3 - z2)^2 - 4r2^2
eq3 = (√Sym(3)*r2/3)^2 + r2^2 + (z2 - h + 3r)^2 - (r + r2)^2
eq4 = dist2(0, h, x, 0, 0, z3, r2);
一度に求められないので,まず eq2, eq3 から \(z_2, z_3\) を求める。
res = solve([eq2, eq3], (z2, z3))[4];
# z2
@show(res[1])
res[1] = (28*sqrt(6)*r^3 + 72*r^3 - 12*sqrt(6)*r^2*r2 - 18*r^2*r2 - 46*sqrt(6)*r*r2^2 - 69*r*r2^2 + (27*r + 18*sqrt(6)*r)*(r + 2*sqrt(6)*r/3 + sqrt(r^2 + 2*r*r2 + 7*r2^2/3 + 4*sqrt(2)*r2*sqrt(3*r^2 + 6*r*r2 - r2^2)/3))^2 - 9*(r + 2*sqrt(6)*r/3 + sqrt(r^2 + 2*r*r2 + 7*r2^2/3 + 4*sqrt(2)*r2*sqrt(3*r^2 + 6*r*r2 - r2^2)/3))^3 + (r + 2*sqrt(6)*r/3 + sqrt(r^2 + 2*r*r2 + 7*r2^2/3 + 4*sqrt(2)*r2*sqrt(3*r^2 + 6*r*r2 - r2^2)/3))*(-36*sqrt(6)*r^2 - 72*r^2 + 54*r*r2 + 15*r2^2))/(18*(r^2 + 2*r*r2 - 3*r2^2))
\(\displaystyle \frac{28 \sqrt{6} r^{3} + 72 r^{3} - 12 \sqrt{6} r^{2} r_{2} - 18 r^{2} r_{2} - 46 \sqrt{6} r r_{2}^{2} - 69 r r_{2}^{2} + \left(27 r + 18 \sqrt{6} r\right) \left(r + \frac{2 \sqrt{6} r}{3} + \sqrt{r^{2} + 2 r r_{2} + \frac{7 r_{2}^{2}}{3} + \frac{4 \sqrt{2} r_{2} \sqrt{3 r^{2} + 6 r r_{2} - r_{2}^{2}}}{3}}\right)^{2} - 9 \left(r + \frac{2 \sqrt{6} r}{3} + \sqrt{r^{2} + 2 r r_{2} + \frac{7 r_{2}^{2}}{3} + \frac{4 \sqrt{2} r_{2} \sqrt{3 r^{2} + 6 r r_{2} - r_{2}^{2}}}{3}}\right)^{3} + \left(r + \frac{2 \sqrt{6} r}{3} + \sqrt{r^{2} + 2 r r_{2} + \frac{7 r_{2}^{2}}{3} + \frac{4 \sqrt{2} r_{2} \sqrt{3 r^{2} + 6 r r_{2} - r_{2}^{2}}}{3}}\right) \left(- 36 \sqrt{6} r^{2} - 72 r^{2} + 54 r r_{2} + 15 r_{2}^{2}\right)}{18 \left(r^{2} + 2 r r_{2} - 3 r_{2}^{2}\right)}\)
# z3
@show(res[2])
res[2] = r + 2*sqrt(6)*r/3 + sqrt(r^2 + 2*r*r2 + 7*r2^2/3 + 4*sqrt(2)*r2*sqrt(3*r^2 + 6*r*r2 - r2^2)/3)
\(\displaystyle r + \frac{2 \sqrt{6} r}{3} + \sqrt{r^{2} + 2 r r_{2} + \frac{7 r_{2}^{2}}{3} + \frac{4 \sqrt{2} r_{2} \sqrt{3 r^{2} + 6 r r_{2} - r_{2}^{2}}}{3}}\)
eq4 の \(z_2,\ z_3\) に求めた解を代入し,条件式 eq4_2 とする。
eq4_2 = eq4(z2 => res[1], z3 => res[2]) |> simplify
\(\displaystyle \frac{10 r^{2}}{9} + \frac{2 r r_{2}}{9} - \frac{2 r \sqrt{9 r^{2} + 18 r r_{2} + 21 r_{2}^{2} + 12 \sqrt{2} r_{2} \sqrt{3 r^{2} + 6 r r_{2} - r_{2}^{2}}}}{9} - \frac{20 r_{2}^{2}}{27} + \frac{4 r_{2} \sqrt{6 r^{2} + 12 r r_{2} - 2 r_{2}^{2}}}{27}\)
eq4_2 を解いて \(r_2\) を求める。
ans_r2 = solve(eq4_2, r2)[1] |> simplify; # 1 of 5
@show(ans_r2)
ans_r2 = 2*r*(3 - sqrt(6))/3
\(\displaystyle \frac{2 r \left(3 - \sqrt{6}\right)}{3}\)
小球の直径 \(2r_2\) は,大球の直径 \(2r\) の \(2(3-\sqrt{6})/3\) 倍である。
27.3 * 2(3 - sqrt(6))/3
10.019286681346163
大球の直径が 27.3 寸のとき,小球の直径は 10.019286681346163 である。
描画関数プログラムのソースを見る
function draw(r, more=true)
pyplot(size=(600, 600), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
a = 2(1 + √6)r
x = a/2√3
h = sqrt(a^2 - a^2/3)
r2 = 2*r*(3 - sqrt(6))/3
z2 = (28*sqrt(6)*r^3 + 72*r^3 - 12*sqrt(6)*r^2*r2 - 18*r^2*r2 - 46*sqrt(6)*r*r2^2 - 69*r*r2^2 + (27*r + 18*sqrt(6)*r)*(r + 2*sqrt(6)*r/3 + sqrt(r^2 + 2*r*r2 + 7*r2^2/3 + 4*sqrt(2)*r2*sqrt(3*r^2 + 6*r*r2 - r2^2)/3))^2 - 9*(r + 2*sqrt(6)*r/3 + sqrt(r^2 + 2*r*r2 + 7*r2^2/3 + 4*sqrt(2)*r2*sqrt(3*r^2 + 6*r*r2 - r2^2)/3))^3 + (r + 2*sqrt(6)*r/3 + sqrt(r^2 + 2*r*r2 + 7*r2^2/3 + 4*sqrt(2)*r2*sqrt(3*r^2 + 6*r*r2 - r2^2)/3))*(-36*sqrt(6)*r^2 - 72*r^2 + 54*r*r2 + 15*r2^2))/(18*(r^2 + 2*r*r2 - 3*r2^2))
z3 = r + 2*sqrt(6)*r/3 + sqrt(r^2 + 2*r*r2 + 7*r2^2/3 + 4*sqrt(2)*r2*sqrt(3*r^2 + 6*r*r2 - r2^2)/3)
@printf("一辺の長さ = %g; 高さ = %g; 球の直径 = %g; x = %g\n", a, h, 2r, x)
p1 = plot([x, 0, -2x, -2x], [0, h, 0, 0],
color=:green, lw=0.5, xlabel="x-axis", ylabel="z-axis")
circle(0, (3 + 2√6)r/3, r)
circle(-2√3r/3, r, r)
circle(√3r/3, r, r)
circle(0, z3, r2, :blue)
circle(-2√3r2/3, z2, r2, :blue)
circle(√3r2/3, z2, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, (3 + 2√6)r/3, "(0,(3+2√6)r/3)", :red)
point(√3r/3, r, "(√3r/3,r)", :red)
point(0, z3, " (0,z3)", :blue, :left, :vcenter)
point(√3r2/3, z2, " (√3r2/3,z2)", :blue, :left, :vcenter)
point(0, h, "h", :green, :center, :bottom, delta=delta)
point(x, 0, "x")
end
p2 = plot([x, x, -2x, x], [-a/2, a/2, 0, -a/2],
color=:green, lw=0.5, xlabel="x-axis", ylabel="y-axis")
rotate(-2r/√3, 0, r)
circle(0, 0, r)
rotate(-2r2/√3, 0, r2, :blue)
circle(0, 0, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(-2r/√3, 0, "(-2r√3/3,0)", :red, :center, delta=-10delta, deltax=5delta)
point(r/√3, r, "(r√3/3,r)", :red, :left, delta=12delta, deltax=3delta)
point(x, a/2, "(x,a/2)", :green, :right, :vcenter, deltax=-3delta)
point(0, 0, "(0,0,(3+2√6)r/3)", :red, :left, delta=-2delta, deltax=delta)
point(-2x, 0, "-2x", :green, :left, :vcenter, deltax=3delta)
xlims!(-2x - 3delta, x + 20delta)
end
plot(p1, p2)
end;
draw(27.3/2, true)
以下のアイコンをクリックして応援してください