六三 埼玉県羽生市須影 八幡神社 慶應元年(1865)
埼玉県立図書館:埼玉県史料集 第二集『埼玉の算額』,昭和44年,誠美堂印刷所,埼玉県与野市.
キーワード:台形,重心
#Julia #SymPy #算額 #和算 #数学
下辺が 8.2 寸の台形を釣り糸で吊るしたとき,下辺が水平になるのは,上辺がいくつのときか。
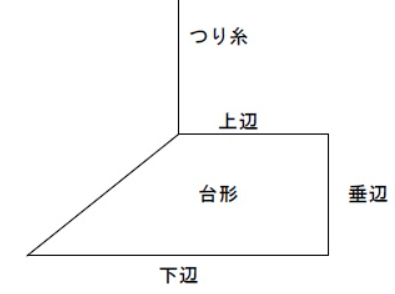
多角形の重心は,その図形を一様な板と考えたときの「面積の中心」である。
頂点が順番に(反時計回りに)与えられた 単純多角形(自己交差しない多角形)については,面積と重心を頂点座標から直接計算できる。
1. 面積の公式
頂点を \( (x_0,y_0),(x_1,y_1),\dots,(x_{n-1},y_{n-1})\) として,最後に最初の頂点に戻るとき,
\(\displaystyle \displaystyle A = \frac{1}{2}\sum_{i=0}^{n-1}(x_i y_{i+1} - x_{i+1} y_i), \quad (x_n,y_n)=(x_0,y_0)\)
で符号付きの面積が求まる。
2. 重心座標の公式
重心の \(x\) 座標と \(y\) 座標は次の式で求められる。
\(\displaystyle \displaystyle C_x = \frac{1}{6A}\sum_{i=0}^{n-1}(x_i+x_{i+1})(x_i y_{i+1} - x_{i+1} y_i)\)
\(\displaystyle \displaystyle C_y = \frac{1}{6A}\sum_{i=0}^{n-1}(y_i+y_{i+1})(x_i y_{i+1} - x_{i+1} y_i)\)
上辺左端 \(A(0, 0)\)
上辺右端 \(B(u, 0)\)
下辺右端 \(C(u, -h)\)
下辺左端 \(D(u - b, -h)\)
とおく。
一様な薄板(面密度一定)と仮定すると,多角形の重心の \(x\) 座標 \(C_x\) は頂点座標から多角形中心の公式で求められ,原点(A)からの \(x\) 成分は次のようになる。
\(\displaystyle C_x=\frac{2u^2 + 2b u - b^2}{3u + 3b}\)
つり糸が上辺左端に取り付くとき上辺と下辺が水平になるためには重心がその真下に来る必要があり,すなわち \(C_x=0\) 。分母は正なので分子を 0 として
\(\displaystyle 2u^2+2b u-b^2=0\) を解けばよい。
using SymPy
@syms u
eq = 2u^2 + 2b*u - b^2
res = solve(eq, u)[1] # 1 of 2
\(\displaystyle b*(-1 + sqrt(3))/2\)
res(b=> 8.2).evalf()
3.00140831103240
上辺は 3.00140831103240 寸である。
以下のアイコンをクリックして応援してください