算額（その1884） - 算額あれこれ

(三-3) 兵庫県伊丹市伊丹桜崎猪名野神社文政11年(1828)

近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日初版第一刷，大阪教育図書株式会社，大阪市.
キーワード：3次元，球，外球，立方体
#Julia #SymPy #算額 #和算 #数学

外球の中に等球 4 個と立方体 1 個を容れる。立方体の一辺の長さは等球の直径と等しい，外球の直径が 1101 寸のとき，等球の直径を得る術を述べよ。

以下の3次元空間の描画では，外球の描画を省略した

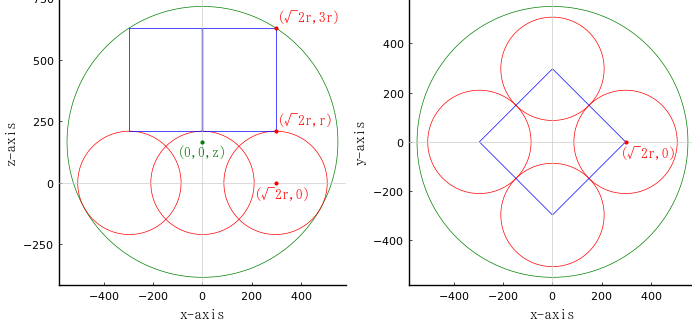
外球の半径と中心座標を \(R, (0, 0, z)\)
等球の半径と中心座標を \(r, (\sqrt{2} r, 0, 0), (-\sqrt{2} r, 0, 0), (0, \sqrt{2} r, 0), (0, \sqrt{2} r, 0)\)
立方体の上面の頂点座標を \( (\sqrt{2} r, 0, 3r), (-\sqrt{2} r, 0, 3r), (0, \sqrt{2} r, 3r), (0, \sqrt{2} r, 3r)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms R::positive, r::positive, z::positive
s2 = sqrt(Sym(2))
eq1 = (s2*r)^2 + z^2 - (R - r)^2
eq2 = (s2*r)^2 + (3r - z)^2 - R^2;

res = solve([eq1, eq2], (r, z))[1] # 1 of 2

( (-133*R + 51*R*(-9/17 + 10*sqrt(2)/17))*(-R + R*(-9/17 + 10*sqrt(2)/17))*(R*(-9/17 + 10*sqrt(2)/17) + R)/(280*R^2), R*(-9/17 + 10*sqrt(2)/17))

# r
ans_r = res[1] |> simplify
@show(ans_r)

ans_r = 2*R*(-1 + 3*sqrt(2))/17

\(\displaystyle \frac{2 R \left(-1 + 3 \sqrt{2}\right)}{17}\)

等球の半径 \(r\) は外球の半径 \(R\) の \(2(3\sqrt{2} -1)/17\) 倍である。

1101 * 2(3√2 -1)/17

420.0173407668628

外球の直径が 1101 寸のとき，等球の直径は 420.0173407668628 寸である。

術は以下のようであり，分母を有理化すれば同じ式であることがわかる。

# 術
@syms 外球径
2*外球径/(sqrt(Sym(18)) + 1)

\(\displaystyle \frac{2 外球径}{1 + 3 \sqrt{2}}\)

2*外球径/(sqrt(Sym(18)) + 1) |> simplify |> factor

\(\displaystyle \frac{2 外球径 \left(-1 + 3 \sqrt{2}\right)}{17}\)

# z
ans_z = res[2] |> factor
@show(ans_z)

ans_z = R*(-9 + 10*sqrt(2))/17

\(\displaystyle \frac{R \left(-9 + 10 \sqrt{2}\right)}{17}\)

描画関数プログラムのソースを見る

function draw(R, more=true)
pyplot(size=(700, 700), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r, z) = (2*R*(-1 + 3*sqrt(2))/17, R*(-9 + 10*sqrt(2))/17)
p1 = plot(xlabel="x-axis", ylabel="z-axis")
circle(0, z, R, :green)
circle2(√2r, 0, r)
circle(0, 0, r)
plot!([√2r, √2r, -√2r, -√2r, √2r], [r, 3r, 3r, r, r], color=:blue, lw=0.5)
segment(0, r, 0, 3r, :blue, lw=1)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, z, "(0,0,z)", :green, :center, delta=-delta)
point(√2r, 0, "(√2r,0)", :red, :center, delta=-delta, deltax=2delta)
point(√2r, r, "(√2r,r)", :red, :left, :bottom, delta=delta, deltax=delta/2)
point(√2r, 3r, "(√2r,3r)", :red, :left, :bottom, delta=delta, deltax=delta/2)
end
p2 = plot(xlabel="x-axis", ylabel="y-axis")
circle(0, 0, R, :green)
circle42(0, √2r, r)
plot!([√2r, 0, -√2r, 0, √2r], [0, √2r, 0, -√2r, 0], color=:blue, lw=0.5)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(√2r, 0, "(√2r,0)", :red, :center, delta=-delta, deltax=6delta)
end
plot(p1, p2)
end;