福島県田村郡三春町山中 田村大元神社 明治34年(1901)
和算の館
http://www.wasan.jp/fukusima/tamuradaigen1.html
キーワード:3次元,球,外球
#Julia #SymPy #算額 #和算 #数学
外球の中に,甲球 2 個,乙球 2 個が入っている。甲球の直径が 3 寸,乙球の直径が 2 寸のとき,外厩の直径はいかほどか。
甲球の直径が 3 寸,乙球の直径が 2 寸の場合には,上下対称になる。
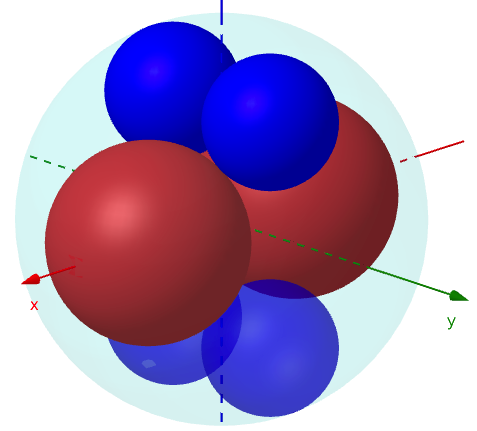
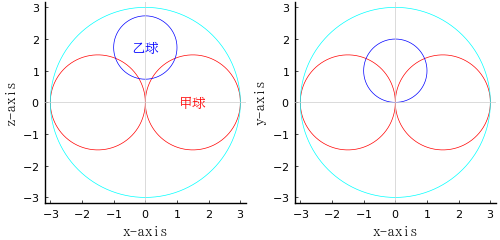
外球の半径と中心座標を \(R,\ (0,\ 0,\ 0)\)
甲球の半径と中心座標を \(r_1,\ (r_1,\ 0,\ z_1)\)
乙球の半径と中心座標を \(r_2,\ (0,\ r_2,\ z_2)\)
とおき,以下の連立方程式を解く。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms R::positive, r1::positive, z1::negative, r2::positive, z2::positive
@syms R::real, r1::real, z1::real, r2::real, z2::real
eq1 = r1^2 + z1^2 - (R - r1)^2
eq2 = r2^2 + z2^2 - (R - r2)^2
eq3 = r1^2 + r2^2 + (z1 - z2)^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3], (R, z1, z2))[1]; # 1 of 4
# R: 外球の半径
ans_R = res[1]
@show(ans_R)
ans_R = (-r1^2*r2^2 - r1*r2^3 - sqrt(6)*sqrt(r1^3*r2^5))/(r2*(r1^2 - 4*r1*r2 + r2^2))
\(\displaystyle \frac{- r_{1}^{2} r_{2}^{2} - r_{1} r_{2}^{3} - \sqrt{6} \sqrt{r_{1}^{3} r_{2}^{5}}}{r_{2} \left(r_{1}^{2} - 4 r_{1} r_{2} + r_{2}^{2}\right)}\)
ans_R(r1 => 3//2, r2 => 2//2)
\(3\)
甲球の直径が 3 寸,乙球の直径が 2 寸のとき,外球の直径は 6 寸である。
# z1: 甲球中心の z 座標
@syms s::positive, t::positive
ans_z1 = res[2](√r1 => s, √r2 => t) |> simplify
@show(ans_z1)
ans_z1 = s^2*t*sqrt( (3*s^6 + 4*sqrt(6)*s^5*t + 2*s^4*t^2 - 6*sqrt(6)*s^3*t^3 - 5*s^2*t^4 + 2*sqrt(6)*s*t^5 + 2*t^6)/(s^8 - 8*s^6*t^2 + 18*s^4*t^4 - 8*s^2*t^6 + t^8))*(sqrt(6)*s^2 - s*t - sqrt(6)*t^2)/(3*s^2 - 2*t^2)
\(\displaystyle \frac{s^{2} t \sqrt{\frac{3 s^{6} + 4 \sqrt{6} s^{5} t + 2 s^{4} t^{2} - 6 \sqrt{6} s^{3} t^{3} - 5 s^{2} t^{4} + 2 \sqrt{6} s t^{5} + 2 t^{6}}{s^{8} - 8 s^{6} t^{2} + 18 s^{4} t^{4} - 8 s^{2} t^{6} + t^{8}}} \left(\sqrt{6} s^{2} - s t - \sqrt{6} t^{2}\right)}{3 s^{2} - 2 t^{2}}\)
ans_z1(s => √(3/2), t => 1).evalf()
\(-3.69504437987417 \cdot 10^{-16}\)
# z2: 乙球中心の z 座標
@syms s::positive, t::positive
ans_z2 = res[3](√r1 => s, √r2 => t) |> factor
@show(ans_z2)
ans_z2 = s*t^2*sqrt( (3*s^6 + 4*sqrt(6)*s^5*t + 2*s^4*t^2 - 6*sqrt(6)*s^3*t^3 - 5*s^2*t^4 + 2*sqrt(6)*s*t^5 + 2*t^6)/(s^8 - 8*s^6*t^2 + 18*s^4*t^4 - 8*s^2*t^6 + t^8))
\(\displaystyle s t^{2} \sqrt{\frac{3 s^{6} + 4 \sqrt{6} s^{5} t + 2 s^{4} t^{2} - 6 \sqrt{6} s^{3} t^{3} - 5 s^{2} t^{4} + 2 \sqrt{6} s t^{5} + 2 t^{6}}{s^{8} - 8 s^{6} t^{2} + 18 s^{4} t^{4} - 8 s^{2} t^{6} + t^{8}}}\)
ans_z2(s => √(3/2), t => 1).evalf()
\(1.73205080756888\)
p = ans_z1/ans_z2
@show(p)
p = s*(sqrt(6)*s^2 - s*t - sqrt(6)*t^2)/(t*(3*s^2 - 2*t^2))
\(\displaystyle \frac{s \left(\sqrt{6} s^{2} - s t - \sqrt{6} t^{2}\right)}{t \left(3 s^{2} - 2 t^{2}\right)}\)
include("julia-source.txt"); # julia-source.txt ソース
using Plots
描画関数プログラムのソースを見る
function draw(r1, r2, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
s = √r1
t = √r2
R = (-r1^2*r2^2 - r1*r2^3 - √6*sqrt(r1^3*r2^5))/(r2*(r1^2 - 4r1*r2 + r2^2))
z2 = s*t^2*sqrt( (3s^6 + 4√6*s^5*t + 2s^4*t^2 - 6√6*s^3*t^3 - 5s^2*t^4 + 2√6*s*t^5 + 2t^6)/(s^8 - 8s^6*t^2 + 18s^4*t^4 - 8s^2*t^6 + t^8))
p = s*(√6s^2 - s*t - √6t^2)/(t*(3s^2 - 2t^2))
z1 = z2*p
p1 = plot(xlabel="x-axis", ylabel="z-axis")
circle2(r1, z1, r1)
circle(0, z2, r2, :blue)
circle(0, 0, R, :cyan)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(r1, 0, "甲球", :red, :center, :vcenter, mark=false)
point(0, z2, "乙球", :blue, :center, :vcenter, mark=false)
end
p2 = plot(xlabel="x-axis", ylabel="y-axis")
circle2(r1, 0, r1)
circle(0, r2, r2, :blue)
circle(0, 0, R, :cyan)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
end
plot(p1, p2)
end;
draw(3/2, 2/2, true)
以下のアイコンをクリックして応援してください