算額（その1719） - 算額あれこれ

深川英俊，ダン・ソコロフスキー：日本の数学ー何題解けますか？[下]，森北出版，1994.

～落書き帳「○△□」～ 391．○△□の新算額（その４）
http://streetwasan.web.fc2.com/math18.1.29.html

キーワード：円3個，二等辺三角形，正方形
#Julia #SymPy #算額 #和算 #数学

下方にある２つの円は半径が等しく，正方形の辺長の 1/4 です。
これらの円に正方形の頂点から接線を引き，正方形の上辺とで二等辺三角形▽を作ります。
このとき，「▽の内接円の半径は，下方の２つの円の半径に等しい」ことを示してください。

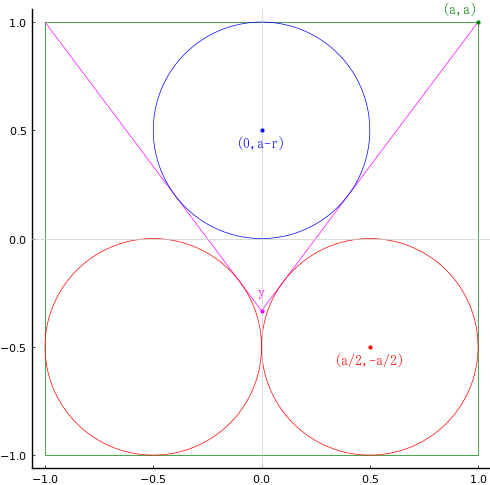
正方形の一辺の長さを \(2a\)
▽の内接円の半径を \(r\)，頂点の座標を \( (0, y); y < 0\)
とおき，以下の連立方程式を解く。

r = a/2 を示せればよい。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms a, r, y
eq1 = dist2(0, y, a, a, 0, a - r, r)
eq2 = dist2(0, y, a, a, a/2, -a/2, a/2)
res = solve([eq1, eq2], (r, y))[2] # 2 of 2

(a/2, -a/3)

# r
res[1] |> println

a/2

\(r\) は \(a/2\) に等しいという結果になった。

描画関数プログラムのソースを見る

function draw(a, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = a/2
y = -a/3
plot([a, a, -a, -a, a], [-a, a, a, -a, -a], color=:green, lw=0.5)
plot!([a, 0, -a], [a, y, a], color=:magenta, lw=0.5)
circle2(a/2, -a/2, a/2)
circle(0, a - r, r, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) / 3 # size[2] * fontsize * 2
vline!([0], color=:gray80, lw=0.5)
hline!([0], color=:gray80, lw=0.5)
point(0, y, "y", :magenta, :center, :bottom, delta=2delta)
point(a/2, -a/2, "(a/2,-a/2)", :red, :center, delta=-delta)
point(0, a - r, "(0,a-r)", :blue, :center, delta=-delta)
point(a, a, "(a,a)", :green, :right, :bottom, delta=delta)
end
end;