福島県白河市明神 境の明神 寛延2年(1749)
~落書き帳「○△□」~ 42.○△□のおにぎり弁当(続々編)
http://streetwasan.web.fc2.com/math15.6.24.html
キーワード:円1個,正三角形,直角三角形,正方形
#Julia #SymPy #算額 #和算 #数学
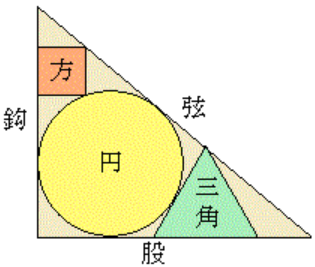
直角三角形の中に,円,正三角形,正方形を図のように内接させる。
鈎の長さと円の半径を与えて,股,弦の長さ,および正三角形と正方形の辺の長さを求めよ。ただし,(鈎の長さ)>(円の直径)とする。
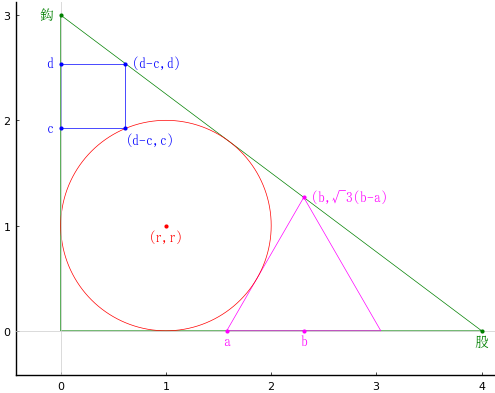
円の半径と中心座標を \(r, (r, r)\)
鈎の上にある正方形の頂点座標を \( (0, c), (0, d); d > c\)
股の上にある正三角形の頂点座標を \( (a, 0), (2b - a); b > a\)
とおき,以下の連立方程式を解く。ただし,一度には解けないので,逐次解いていく。
まず,eq1, eq5 は単独の方程式として解くことができる。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms 鈎::positive, 股::positive, r::positive,
a::positive, b::positive, c::positive, d::positive
eq1 = √Sym(3)*(b - a)/(股 - b) - 鈎/股
eq2 = ( (d - c) - r)^2 + (c - r)^2 - r^2
eq3 = 鈎 + 股 - sqrt(鈎^2 + 股^2) - 2r
eq4 = d/(股 - (d - c)) - 鈎/股
eq5 = dist2(a, 0, b, √Sym(3)*(b - a), r, r, r);
# res = solve([eq1, eq2, eq3, eq4, eq5], (股, a, b, c, d))
# 股
ans_股 = solve(eq3, 股)[1]
ans_股 |> println
ans_股 |> display
2*r*(r - 鈎)/(2*r - 鈎)
\( \displaystyle \frac{2 r \left(r - 鈎\right)}{2 r - 鈎}\)
鈎が 3,円の半径が 1 のとき,股は 2(1 - 3)/(2 - 3) = 4 である。
# 弦
弦 = sqrt(鈎^2 + ans_股^2) |> simplify
弦 |> println
弦 |> display
sqrt(4*r^2*(r - 鈎)^2 + 鈎^2*(2*r - 鈎)^2)/Abs(2*r - 鈎)
\( \displaystyle \frac{\sqrt{4 r^{2} \left(r - 鈎\right)^{2} + 鈎^{2} \left(2 r - 鈎\right)^{2}}}{\left|{2 r - 鈎}\right|}\)
鈎が 3,円の半径が 1 のとき,弦は 5 である。
弦(鈎 => 3, r => 1) |> println
5
# a
ans_a = solve(eq5, a)[1]
ans_a |> println
ans_a |> display
r*(sqrt(3) + 3)/3
\( \displaystyle \frac{r \left(\sqrt{3} + 3\right)}{3}\)
eq1, eq2, eq5 の 股,\(a\) に上で求められた結果を代入し,新たな方程式を得る。
eq11 = eq1(股 => ans_股, a => ans_a) |> simplify |> numerator |> x -> x/(2r - 鈎) |> expand
\( \displaystyle - 6 \sqrt{3} b r^{2} - 6 b r 鈎 + 6 \sqrt{3} b r 鈎 + 3 b 鈎^{2} + 6 r^{3} + 6 \sqrt{3} r^{3} - 6 \sqrt{3} r^{2} 鈎 - 6 r 鈎^{2}\)
eq12 = eq2 |> expand
\( \displaystyle 2 c^{2} - 2 c d + d^{2} - 2 d r + r^{2}\)
eq14 = eq4(股 => ans_股) |> expand |> simplify |> numerator |> simplify |> x -> x/(r - 鈎/2) |> expand
\( \displaystyle - 2 c r 鈎 + c 鈎^{2} + 2 d r^{2} - d 鈎^{2} - 2 r^{2} 鈎 + 2 r 鈎^{2}\)
eq11, eq12, eq14 を 3 元連立方程式として解く。
res1 = solve([eq11, eq12, eq14], (b, c, d))[1] # 1 of 2
(2*r^3/(2*sqrt(3)*r^2 - 2*sqrt(3)*r*鈎 + 2*r*鈎 - 鈎^2) + 2*sqrt(3)*r^3/(2*sqrt(3)*r^2 - 2*sqrt(3)*r*鈎 + 2*r*鈎 - 鈎^2) - 2*sqrt(3)*r^2*鈎/(2*sqrt(3)*r^2 - 2*sqrt(3)*r*鈎 + 2*r*鈎 - 鈎^2) - 2*r*鈎^2/(2*sqrt(3)*r^2 - 2*sqrt(3)*r*鈎 + 2*r*鈎 - 鈎^2), (-2*r^2*鈎 + 2*r*鈎^2 + (2*r^2 - 鈎^2)*(-2*sqrt(2)*r^(3/2)*鈎*sqrt(-(r - 鈎)^3)*(2*r - 鈎)/(8*r^4 - 8*r^3*鈎 + 鈎^4) + r*鈎*(8*r^3 - 8*r^2*鈎 - 2*r*鈎^2 + 3*鈎^3)/(8*r^4 - 8*r^3*鈎 + 鈎^4)))/(鈎*(2*r - 鈎)), -2*sqrt(2)*r^(3/2)*鈎*sqrt(-(r - 鈎)^3)*(2*r - 鈎)/(8*r^4 - 8*r^3*鈎 + 鈎^4) + r*鈎*(8*r^3 - 8*r^2*鈎 - 2*r*鈎^2 + 3*鈎^3)/(8*r^4 - 8*r^3*鈎 + 鈎^4))
# b
ans_b = res1[1] |> simplify
ans_b |> println
ans_b
2*r*(r^2 + sqrt(3)*r^2 - sqrt(3)*r*鈎 - 鈎^2)/(2*sqrt(3)*r^2 - 2*sqrt(3)*r*鈎 + 2*r*鈎 - 鈎^2)
\( \displaystyle \frac{2 r \left(r^{2} + \sqrt{3} r^{2} - \sqrt{3} r 鈎 - 鈎^{2}\right)}{2 \sqrt{3} r^{2} - 2 \sqrt{3} r 鈎 + 2 r 鈎 - 鈎^{2}}\)
# c
ans_c = res1[2] |> simplify
ans_c |> println
ans_c |> display
(-2*r*(r - 鈎)*(8*r^4 - 8*r^3*鈎 + 鈎^4) - (2*r^2 - 鈎^2)*(2*sqrt(2)*r^(3/2)*sqrt(-(r - 鈎)^3)*(2*r - 鈎) - r*(8*r^3 - 8*r^2*鈎 - 2*r*鈎^2 + 3*鈎^3)))/( (2*r - 鈎)*(8*r^4 - 8*r^3*鈎 + 鈎^4))
\( \displaystyle \frac{- 2 r \left(r - 鈎\right) \left(8 r^{4} - 8 r^{3} 鈎 + 鈎^{4}\right) - \left(2 r^{2} - 鈎^{2}\right) \left(2 \sqrt{2} r^{\frac{3}{2}} \sqrt{- \left(r - 鈎\right)^{3}} \left(2 r - 鈎\right) - r \left(8 r^{3} - 8 r^{2} 鈎 - 2 r 鈎^{2} + 3 鈎^{3}\right)\right)}{\left(2 r - 鈎\right) \left(8 r^{4} - 8 r^{3} 鈎 + 鈎^{4}\right)}\)
# d
ans_d = res1[3] |> simplify
ans_d |> println
ans_d |> display
鈎*(-2*sqrt(2)*r^(3/2)*sqrt(-(r - 鈎)^3)*(2*r - 鈎) + r*(8*r^3 - 8*r^2*鈎 - 2*r*鈎^2 + 3*鈎^3))/(8*r^4 - 8*r^3*鈎 + 鈎^4)
\( \displaystyle \frac{鈎 \left(- 2 \sqrt{2} r^{\frac{3}{2}} \sqrt{- \left(r - 鈎\right)^{3}} \left(2 r - 鈎\right) + r \left(8 r^{3} - 8 r^{2} 鈎 - 2 r 鈎^{2} + 3 鈎^{3}\right)\right)}{8 r^{4} - 8 r^{3} 鈎 + 鈎^{4}}\)
正方形の一辺の長さは \(d - c\) である。\(sq = d - c\) とする。
sq = ans_d - ans_c |> factor
\( \displaystyle \frac{2 \left(4 \sqrt{2} r^{\frac{9}{2}} \sqrt{- r^{3} + 3 r^{2} 鈎 - 3 r 鈎^{2} + 鈎^{3}} - 6 \sqrt{2} r^{\frac{7}{2}} 鈎 \sqrt{- r^{3} + 3 r^{2} 鈎 - 3 r 鈎^{2} + 鈎^{3}} + 2 \sqrt{2} r^{\frac{5}{2}} 鈎^{2} \sqrt{- r^{3} + 3 r^{2} 鈎 - 3 r 鈎^{2} + 鈎^{3}} + 2 r^{4} 鈎^{2} - 5 r^{3} 鈎^{3} + 4 r^{2} 鈎^{4} - r 鈎^{5}\right)}{\left(2 r - 鈎\right) \left(8 r^{4} - 8 r^{3} 鈎 + 鈎^{4}\right)}\)
鈎が 3,円の半径が 1 のとき,正方形の一辺の長さは 8/13 = 0.615384615384615 である。
sq(鈎 => 3, r => 1)
\( \displaystyle \frac{8}{13}\)
sq(鈎 => 3, r => 1).evalf() |> println
0.615384615384615
正三角形の一辺の長さは \(2(b - a)\) である。\(tri = 2(b - a)\) とする。
tri = 2(ans_b - ans_a) |> simplify
\( \displaystyle \frac{2 r 鈎 \left(- 2 \sqrt{3} r - 3 鈎 + \sqrt{3} 鈎\right)}{3 \left(2 \sqrt{3} r^{2} - 2 \sqrt{3} r 鈎 + 2 r 鈎 - 鈎^{2}\right)}\)
鈎が 3,円の半径が 1 のとき,正三角形の一辺の長さは 1.46410161513775 である。
tri(鈎 => 3, r => 1)
\( \displaystyle \frac{2 \left(-9 + \sqrt{3}\right)}{- 4 \sqrt{3} - 3}\)
tri(鈎 => 3, r => 1).evalf() |> println
1.46410161513775
描画関数プログラムのソースを見る
function draw(鈎, r, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(股, a, b, c, d) = [2.0, 0.7886751345948129, 1.1547005383792515, 0.9615384615384616, 1.2692307692307692]
股 = 2*r*(r - 鈎)/(2*r - 鈎)
弦 = sqrt(鈎^2 + 股^2)
a = r*(sqrt(3) + 3)/3
b = 2*r*(r^2 + sqrt(3)*r^2 - sqrt(3)*r*鈎 - 鈎^2)/(2*sqrt(3)*r^2 - 2*sqrt(3)*r*鈎 + 2*r*鈎 - 鈎^2)
c = (-2*r*(r - 鈎)*(8*r^4 - 8*r^3*鈎 + 鈎^4) - (2*r^2 - 鈎^2)*(2*sqrt(2)*r^(3/2)*sqrt(-(r - 鈎)^3)*(2*r - 鈎) - r*(8*r^3 - 8*r^2*鈎 - 2*r*鈎^2 + 3*鈎^3)))/( (2*r - 鈎)*(8*r^4 - 8*r^3*鈎 + 鈎^4))
d = 鈎*(-2*sqrt(2)*r^(3/2)*sqrt(-(r - 鈎)^3)*(2*r - 鈎) + r*(8*r^3 - 8*r^2*鈎 - 2*r*鈎^2 + 3*鈎^3))/(8*r^4 - 8*r^3*鈎 + 鈎^4)
@printf("鈎が %g,円の半径が %g のとき,股は %g,弦は %g,正方形の一辺の長さは %g, 正三角形の一辺の長さは %g である。\n", 鈎, r, 股, 弦, d - c, 2(b - a))
plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
plot!([a, 2b - a, b, a], [0, 0, √3(b - a), 0], color=:magenta, lw=0.5)
circle(r, r, r)
rect(0, c, d - c, d, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) / 3 # size[2] * fontsize * 2
vline!([0], color=:gray80, lw=0.5)
hline!([0], color=:gray80, lw=0.5)
point(a, 0, "a", :magenta, :center, delta=-delta)
point(b, 0, "b", :magenta, :center, delta=-delta)
point(股, 0, "股", :green, :center, delta=-delta)
point(b, √3(b - a), " (b,√3(b-a)", :magenta, :left, :vcenter)
point(0, c, "c ", :blue, :right, :vcenter)
point(0, d, "d ", :blue, :right, :vcenter)
point(0, 鈎, "鈎 ", :green, :right, :vcenter)
point(d - c, d, " (d-c,d)", :blue, :left, :vcenter)
point(d - c, c, "(d-c,c)", :blue, :left, delta=-delta)
point(r, r, "(r,r)", :red, :center, delta=-delta)
plot!(xlims=(-10delta, 股 + 3delta), ylims=(-10delta, 鈎 + 3delta))
end
end;
draw(3, 1, true)
draw(3, 1.2, true)
以下のアイコンをクリックして応援してください