算額（その484） - 算額あれこれ

宮城県丸森町小斎日向鹿島神社明治13年(1880)

徳竹亜紀子，谷垣美保: 2022年度の算額調査，仙台高等専門学校名取キャンパス研究紀要，第 59 号, p.9-47, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp-content/uploads/2023/05/kiyo2023-2.pdf
キーワード：円4個，外円
#Julia #SymPy #算額 #和算 #数学

外円内に甲円，乙円，丙円が入っている。3 個の円の中心は鈎股弦（直角三角形）を作る。鈎が 3 寸，股が 4 寸のとき，外円の直径はいかほどか。

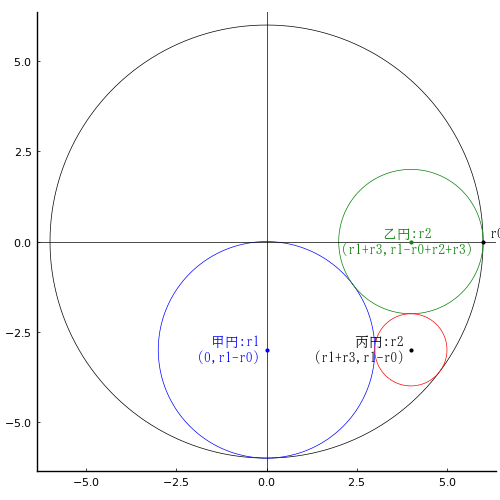
外円の半径と中心座標を \(r_0,\ (0,\ 0);\ r_0 = 6r_2\)
甲円の半径と中心座標を \(r_1,\ (0,\ r_1 - r_0)\)
乙円の半径と中心座標を \(r_2,\ (r_1 + r_3,\ r_1 - r_0 + r_2 + r_3)\)
丙円の半径と中心座標を \(r_3,\ (r_1 + r_3,\ r_1 - r_0)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms r0::positive, r1::positive, r2::positive,
r3::positive, 鈎::positive, 股::positive;

eq1 = r2 + r3 - 鈎
eq2 = r1 + r3 - 股
eq3 = (r1 + r2)^2 -(鈎^2 + 股^2)
eq4 = (r1 + r3)^2 + (r1 - r0)^2 - (r0 - r3)^2
solve([eq1, eq2, eq3, eq4], (r0, r1, r2, r3))[2] # 2 of 2

(股/2 + 鈎/2 + sqrt(股^2 + 鈎^2)/2, 股/2 - 鈎/2 + sqrt(股^2 + 鈎^2)/2, -股/2 + 鈎/2 + sqrt(股^2 + 鈎^2)/2, 股/2 + 鈎/2 - sqrt(股^2 + 鈎^2)/2)

外円の半径は \(\displaystyle \frac{股}{2} + \frac{鈎}{2} + \frac{\sqrt{股^{2} + 鈎^{2}}}{2}\) なので，直径は \(\displaystyle 股 + 鈎 + \sqrt{股^{2} + 鈎^{2}}\) である。さらに，\(\displaystyle \sqrt{股^{2} + 鈎^{2}} = 弦 \) なので，外円の直径は鈎，股，弦の和になる。
鈎 = 3, 股 = 4 のとき，弦 = 5 なので，外円の直径は 12 である。

その他，\(r_1,\ r_2,\ r_3\) は以下のようになる。

\(\displaystyle r_1 = \frac{弦}{2} + \frac{股}{2} - \frac{鈎}{2}\)

\(\displaystyle r_2 = \frac{弦}{2} - \frac{股}{2} + \frac{鈎}{2}\)

\(\displaystyle r_3 = \frac{ - 弦}{2} + \frac{股}{2} + \frac{鈎}{2}\)

\(r_0 = 6;\ r_1 =　3;\ r_2 =　2;\ r_3 =　1\)
\(鈎 = 3;\ 股 = 4;\ 弦 = 5;\ 外円の直径 = 12\)

外円の直径(鈎, 股) = 鈎 + 股 + sqrt(鈎^2 + 股^2) # 鈎，股を与えて外円の直径を求める関数
外円の直径(3, 4) |> println
外円の直径(3, 7) |> println

12.0
17.61577310586391

描画関数プログラムのソースを見る

function draw(鈎, 股, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
弦 = sqrt(鈎^2 + 股^2)
(r0, r1, r2, r3) = ( (股 + 鈎 + 弦)/2, (股 - 鈎 + 弦)/2, (-股 + 鈎 + 弦)/2, (股 + 鈎 - 弦)/2)
@printf("r0 = %g; r1 =　%g; r2 =　%g; r3 =　%g\n", r0, r1, r2, r3)
@printf("鈎 = %g; 股 = %g; 弦 = %g; 外円の直径 = %g\n", 鈎, 股, 弦, 2r0)
plot()
circle(0, 0, r0, :black)
circle(0, r1 - r0, r1, :blue)
circle(r1 + r3, r1 - r0 + r2 + r3, r2, :green)
circle(r1 + r3, r1 - r0, r3)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(0, r1 - r0, "甲円:r1 \n(0,r1-r0) ", :blue, :right, :vcenter)
point(r1 + r3, r1 - r0 + r2 + r3, "乙円:r2 \n(r1+r3,r1-r0+r2+r3) ", :green, :center, :vcenter)
point(r1 + r3, r1 - r0, "丙円:r2 \n(r1+r3,r1-r0) ", :black, :right, :vcenter)
point(r0, 0, " r0", :black, :left, :bottom, delta=delta/3)
end
end;