算額（その1055）旧版 - 算額あれこれ

改定第2版を書きました。

岩手県陸前高田市小友町谷地館八幡神社明治26年(1893)

今有如図(03079)
https://w.atwiki.jp/sangaku/pages/283.html

安富有恒：和算—岩手の現存算額のすべて（91），青磁社，東京都，1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf

山村善夫：現存岩手の算額（九十一），昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

キーワード：円5個，直角三角形，正方形
#Julia #SymPy #算額 #和算 #数学

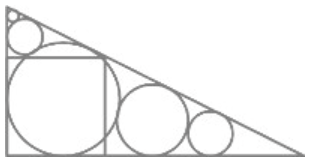
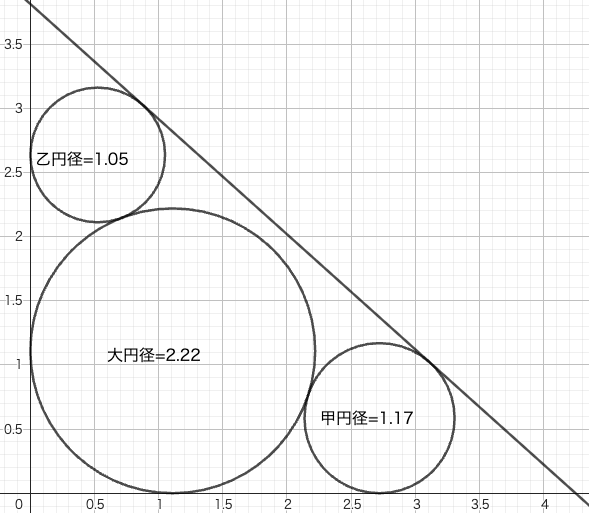
直角三角形内に正方形と大円，甲円，乙円，丙円，丁円を容れる。甲円，乙円の直径がそれぞれ 1.17 寸，1.05 寸のとき，大円の直径はいかほどか。

この算額図において，正方形はなんの意味もない。丙円，丁円も不要なものである。また，図に示された甲円と乙円の大きさの比は，問で与えられたものと異なっている。
確認できる 3 資料で，図は少しずつ差がある。
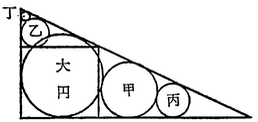
安富のものは乙円の位置が不安定である。
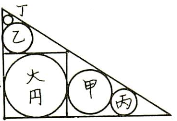
山村のものは大円が正方形の中に入っている。そのような仮定の下での解は，術と一致しない。
最も適切なのは「今有如図」のものであろう。

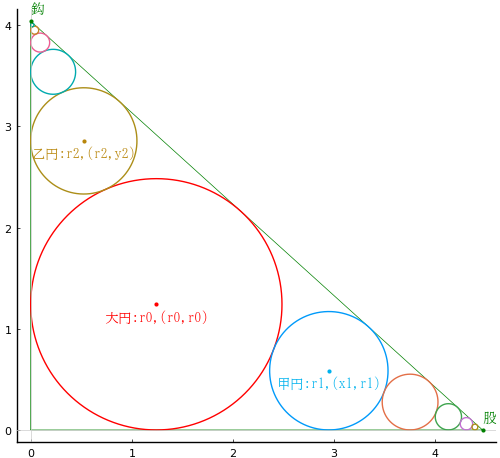
大円の半径と中心座標を \(r_0,\ (r_0,\ r_0)\)
甲円の半径と中心座標を \(r_1,\ (r_0 + 2\sqrt{r_0 r_1},\ r_1)\)
乙円の半径と中心座標を \(r_2,\ (r_2,\ r_0 + 2\sqrt{r_0 r_2},\ r_2)\)
とおき，以下の連立方程式を解く。

eq1 は，大円から始まり，甲円，丙円，... が相似な累円であること，
eq2 は，大円から始まり，乙円，丁円，... が相似な累円であること，
eq3 は，直角三角形の内接円における，3 辺と直径の関係の式である。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
r0, r1::positive, r2::positive
弦 = sqrt(鈎^2 + 股^2)
eq1 = r0/(股 - r0) - r1/(股 - r0 - 2sqrt(r0*r1))
eq2 = r0/(鈎 - r0) - r2/(鈎 - r0 - 2sqrt(r0*r2))
eq3 = 鈎 + 股 - 弦 - 2r0;
# res = solve([eq1, eq2, eq3], (鈎, 股, r0))

eq1, eq2 はそれぞれ個別に股，鈎を求めることができる。

ans_股 = solve(eq1, 股)[1]

\(\displaystyle \frac{2 r_{0}^{\frac{3}{2}} \sqrt{r_{1}} + r_{0}^{2} - r_{0} r_{1}}{r_{0} - r_{1}}\)

ans_鈎 = solve(eq2, 鈎)[1]

\(\displaystyle \frac{2 r_{0}^{\frac{3}{2}} \sqrt{r_{2}} + r_{0}^{2} - r_{0} r_{2}}{r_{0} - r_{2}}\)

得られた解を eq3 に代入すれば，\(r_0\) を含む方程式になる（股，鈎は既知）。

eq3_2 = eq3(鈎 => ans_鈎, 股 => ans_股)

\(\displaystyle - 2 r_{0} - \sqrt{\frac{\left(2 r_{0}^{\frac{3}{2}} \sqrt{r_{2}} + r_{0}^{2} - r_{0} r_{2}\right)^{2}}{\left(r_{0} - r_{2}\right)^{2}} + \frac{\left(2 r_{0}^{\frac{3}{2}} \sqrt{r_{1}} + r_{0}^{2} - r_{0} r_{1}\right)^{2}}{\left(r_{0} - r_{1}\right)^{2}}} + \frac{2 r_{0}^{\frac{3}{2}} \sqrt{r_{2}} + r_{0}^{2} - r_{0} r_{2}}{r_{0} - r_{2}} + \frac{2 r_{0}^{\frac{3}{2}} \sqrt{r_{1}} + r_{0}^{2} - r_{0} r_{1}}{r_{0} - r_{1}}\)

SYmPy では解けないので，find_zero() を用いて数値解を求める。

using Roots
ans_r0 = find_zero(eq3_2(r1 => 1.17/2, r2 => 1.05/2), (1, 3))

1.241635304307822

大円の直径は 2.483270608615644 寸である。

この図に基づいてもやはり，答の 2.22 寸にならず，術の「甲円と乙円の直径を加えれば大円の直径になる」こともない。

前段階で求められた ans_鈎, ans_股にans_r0 を代入すれば数値解が得られる。

ans_鈎(r1 => 1.17/2, r2 => 1.05/2, r0 => 1.2416353043078219) |> println
ans_股(r1 => 1.17/2, r2 => 1.05/2, r0 => 1.2416353043078219) |> println

4.03934422082295
4.46474271483139

算額の言うような，甲円，乙円の直径がそれぞれ 1.17 寸，1.05 寸で，大円の直径が 2.22 寸では，図が成り立たない。

描画関数プログラムのソースを見る

function nextcircle(r0, r1; y=false)
p = r1/r0
x0 = r0
for i = 1:5
ri = p*r0
x0 += 2sqrt(r0*ri)
y && circle(ri, x0, ri, i + 4, lw=1)
y || circle(x0, ri, ri, i, lw=1)
r0 = ri
end
end;

function draw(r1, r2, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(鈎, 股, r0) = [4.03934422082295, 4.46474271483139, 1.2416353043078219]
弦 = sqrt(鈎^2 + 股^2)
println(2r0)
plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
circle(r0, r0, r0, lw=1)
nextcircle(r0, r1)
nextcircle(r0, r2; y=true)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(r0, r0, "大円:r0,(r0,r0)", :red, :center, delta=-delta)
point(r0 + 2sqrt(r0*r1), r1, "甲円:r1,(x1,r1)", :deepskyblue2, :center, delta=-delta)
point(r2, r0 + 2sqrt(r0*r2), "乙円:r2,(r2,y2)", :darkgoldenrod, :center, delta=-delta)
point(股, 0, "股", :green, :left, :bottom, delta=delta)
point(0, 鈎, "鈎", :green, :left, :bottom, delta=delta)
end
end;