算額（その485） - 算額あれこれ

宮城県丸森町小斎日向鹿島神社弘化5年(1848)

徳竹亜紀子，谷垣美保: 2022年度の算額調査，仙台高等専門学校名取キャンパス研究紀要，第 59 号, p.9-47, 2022.
https://www.sendai-nct.ac.jp/natori-library/wp-content/uploads/2023/05/kiyo2023-2.pdf
キーワード：円12個，楕円
#Julia #SymPy #算額 #和算 #数学

楕円の中に大円，中円，小円が入っている。楕円の短径(短軸の半分;図参照)が与えられたとき，小円の直径を求めよ。

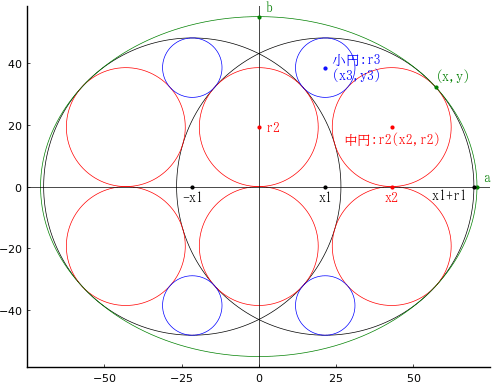
大円の半径と中心座標を \(r_1, (x_1, 0), (-x_1, 0)\)
中円の半径と中心座標を\( r_2, (0, r_2), (x_2, r_2)\)
小円の半径と中心座標を \(r_3, (x_3, y_3)\)
楕円の長径と短径を \(a, b\)
楕円と右上の中円の接点を \( (x, y)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms a::positive, b::positive,
x::positive, y::positive,
r1::positive, x1::positive,
r2::positive, x2::positive,
r3::positive, x3::positive, y3::positive;

b = 55
x3 = x1
x2 = 2x1
eq1 = (x3 - x1)^2 + y3^2 - (r1 - r3)^2
eq2 = x1^2 + r2^2 - (r1 - r2)^2 # 算法助術の公式84
eq3 = (x3 + x1)^2 + y3^2 - (r1 + r3)^2
eq4 = (x1 + x2)^2 + r2^2 - (r1 + r2)^2
eq5 = (x2 - x3)^2 + (y3 - r2)^2 - (r2 + r3)^2
eq6 = (x - x1)^2 + y^2 - r1^2
eq7 = (x - x2)^2 + (y - r2)^2 - r2^2
eq8 = x^2/a^2 + y^2/b^2 - 1;
#res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8], (a, r1, x1, r2, r3, y3, x, y))

y3^2 - (r1 - r3)^2, # eq1
4*x1^2 - (3025 - r1^2)*(4*a^2 - 12100)/3025, # eq2
4*x1^2 + y3^2 - (r1 + r3)^2, # eq3
r2^2 + 9*x1^2 - (r1 + r2)^2, # eq4
x1^2 + (-r2 + y3)^2 - (r2 + r3)^2, # eq5
-r1^2 + y^2 + (x - x1)^2, # eq6
-r2^2 + (-r2 + y)^2 + (x - 2*x1)^2, # eq7
y^2/3025 - 1 + x^2/a^2, # eq8

function H(u)
(a, r1, x1, r2, r3, y3, x, y) = u
return [
y3^2 - (r1 - r3)^2, # eq1
r2^2 + x1^2 - (r1 - r2)^2, # eq2
4*x1^2 + y3^2 - (r1 + r3)^2, # eq3
r2^2 + 9*x1^2 - (r1 + r2)^2, # eq4
x1^2 + (-r2 + y3)^2 - (r2 + r3)^2, # eq5
-r1^2 + y^2 + (x - x1)^2, # eq6
-r2^2 + (-r2 + y)^2 + (x - 2*x1)^2, # eq7
y^2/3025 - 1 + x^2/a^2, # eq8
]
end;

b = 55
iniv = [big"73.0", 49, 22, 19.5, 10, 39, 56, 35]
res = nls(H, ini=iniv)

([69.57010852370435, 47.63139720814412, 21.301408404140794, 19.05255888325765, 9.526279441628825, 38.1051177665153, 56.80375574437545, 31.75426480542942], false)

短径が 55 のとき，小円の直径 = 19.05255888325765 となる。

術では短径sqrt(3)/5 となっており，短径 = 55 のときには小円の直径は 19.05255888325765 になるので，上で得られた解は正しいものである。

55sqrt(3)/5

19.05255888325765

描画関数プログラムのソースを見る

function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
b = 55
(a, r1, x1, r2, r3, y3, x, y) = res[1]
x3 = x1
x2 = 2x1
@printf("a = %g; r1 = %g; x1 = %g; r2 = %g; r3 = %g; y3 = %g; x = %g; y = %g\n",
a, r1, x1, r2, r3, y3, x, y)
@printf("小円の直径 = %g\n", 2r3)
plot()
circle(x1, 0, r1, :black)
circle(-x1, 0, r1, :black)
circle4(x2, r2, r2)
circle(0, r2, r2)
circle(0, -r2, r2)
circle4(x3, y3, r3, :blue)
ellipse(0, 0, a, b, color=:green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(x, y, "(x,y)", :green, :left, :bottom, delta=delta)
point(x1, 0, "x1", :black, :center, delta=-delta)
point(-x1, 0, "-x1", :black, :center, delta=-delta)
point(x2, 0, "x2", :red, :center, delta=-delta)
point(0, r2, " r2", :red, :left, :vcenter)
point(x3, y3, " 小円:r3\n (x3,y3)", :blue, :left, :vcenter)
point(x2, r2, "中円:r2(x2,r2)", :red, :center, delta=-delta)
point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
point(x1 + r1, 0, "x1+r1 ", :black, :right, :top, delta=-delta/2)
point(0, b, " b", :green, :left, :bottom, delta=delta/2)
end
end;