算額（その66） - 算額あれこれ

東京都中央区茅場町薬師堂寛政元年(1789)6月

和算の館
http://www.wasan.jp/tokyo/yakusi.html

福島県白河市鹿島鹿島神社寛政3年(1791)

和算の館
http://www.wasan.jp/fukusima/kashima1.html

長野県長野市鬼無里松厳寺天保10年(1839)

中村信弥「改訂増補長野県の算額」県内の算額(P.147)
http://www.wasan.jp/zoho/zoho.html

キーワード：円7個，外円
#Julia #SymPy #算額 #和算 #数学

甲円，乙円の径がそれぞれ 69 寸，23 寸である。外円の径を求めよ。

図のように記号を定め，方程式を解く。

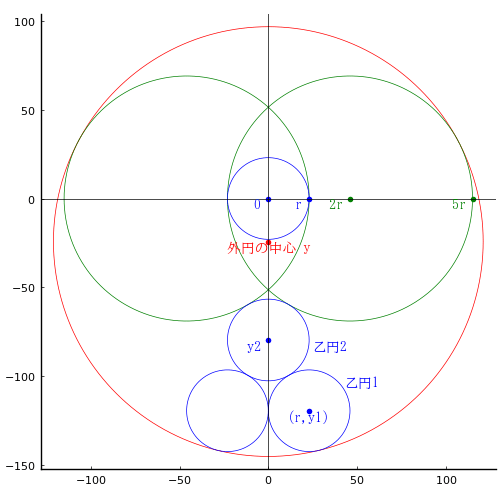
注：外円の中心は乙円の円周上にあるのではない。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms y::negative, y1::negative, y2::negative, R::positive;
r = 23
eq0 = y2 - y1 - r*sqrt(Sym(3));
eq1 = 4r^2 + y2^2 - 16r^2 # 甲円と乙円2が外接する
eq2 = r^2 + (y - y1)^2 - (R - r)^2 # 外円と乙円1が内接する
eq3 = 4r^2 + y^2 - (R - 3r)^2; # 外円と甲円が内接する
res = solve([eq0, eq1, eq2, eq3], (y, y1, y2, R))[1]

(-14*sqrt(3), -69*sqrt(3), -46*sqrt(3), 121)

\(R\) は 121 となった。

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
plot()
r = 23
(y, y1, y2, R) = (-14*sqrt(3), -69*sqrt(3), -46*sqrt(3), 121)
circle(0, y, R)
circle2(2r, 0, 3r, :green)
circle(0, 0, r, :blue)
circle(0, y2, r, :blue)
circle2(r, y1, r, :blue)
if more
point(0, 0, "0 ", :blue, :right)
point(r, 0, "r ", :blue, :right)
point(0, y, "外円の中心 y", :red, :center)
point(2r, 0, "2r ", :green, :right)
point(5r, 0, "5r ", :green, :right)
point(r, y1, "(r,y1)", :blue, :center)
point(0, y2, "y2 ", :blue, :right)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(25, -80, "小円2", :blue, mark=false)
point(43, -100, "小円1", :blue, mark=false)
end
end;