算額（その1499） - 算額あれこれ

50 岩手県一関市弥栄字北ノ沢白山神社慶應2年(1866)

安富有恒：和算—岩手の現存算額のすべて，青磁社，東京都，1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード：円3個，円弧
#Julia #SymPy #算額 #和算 #数学

直径が同じ 2 個の円弧が交差してできる月形の中に等円 3 個を容れる。等円の直径が 873 寸のとき，円弧の直径はいかほどか。
注：左側の円弧は右側の円弧の中心を通る。

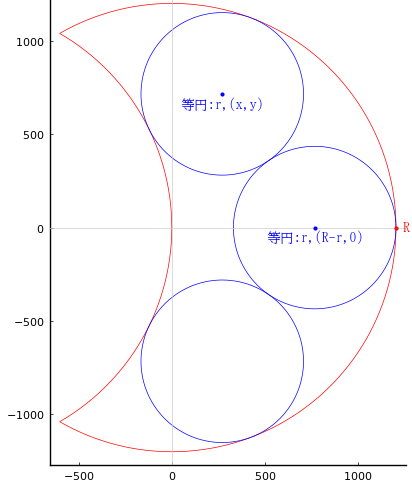
円弧の半径と中心座標を \(R, (0, 0), (-R, 0)\)
等円の半径と中心座標を \(r, (R - r, 0), (x, y)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms R::positive, r::positive, x::positive, y::positive
eq1 = x^2 + y^2 - (R - r)^2
eq2 = (R - r - x)^2 + y^2 - 4r^2
eq3 = (R + x)^2 + y^2 - (R + r)^2
res = solve([eq1, eq2, eq3], (R, x, y))[1]

(r*(sqrt(57) + 9)/6, r*(15 - sqrt(57))/12, r*sqrt(-1/8 + 3*sqrt(57)/8))

円弧の半径 \(R\) は，等円の半径 \(r\) の \( (\sqrt{57} + 9)/6\) 倍である。
等円の直径が 873 寸のとき，円弧の半径は \(873(\sqrt{57} + 9)/6 = 2408.000910331894\) 寸である。

描画関数プログラムのソースを見る

function draw(r, more=false)
pyplot(size=(500, 500), showaxis=true, grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, x, y) = (r*(sqrt(57) + 9)/6, r*(15 - sqrt(57))/12, r*sqrt(-1/8 + 3*sqrt(57)/8))
@printf("等円の直径が %gのとき，円弧の直径は %g である。\n", 2r, 2R)
plot()
circle(0, 0, R, beginangle=240, endangle=480)
circle(-R, 0, R, beginangle=300, endangle=420)
circle22(x, y, r, :blue)
circle(R - r, 0, r, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(R, 0, " R", :red, :left, :vcenter)
point(R - r, 0, "等円:r,(R-r,0)", :blue, :center, delta=-delta/2)
point(x, y, "等円:r,(x,y)", :blue, :center, delta=-delta/2)
end
end;