続神壁算法 付録〇三 東都芝増上寺境内内天満宮 寛政11年(1799)
豫州松山 丸山良玄門人 大西佐兵衛義全
平田浩一:大西佐兵衛著『雑題』の研究--第1巻より--,松山大学論集,第33巻第1号,2021年4月.
https://ehimewasan.com/wp-content/uploads/2024/12/6dba4f7ea9ead10da8d07ad8ddcf8d4a.pdf
キーワード:円2個,外円,正方形
#Julia #SymPy #算額 #和算 #数学
円弧の中に,大小の正方形と円を容れる。大正方形の一辺の長さが 11.31 寸,円の直径が 7.54 寸のとき,小正方形の一辺の長さはいかほどか。
この図形は算法助術の公式33 に取り上げられたものと基本的に同じであるが,平田の論文が最も丁寧でわかりやすい。
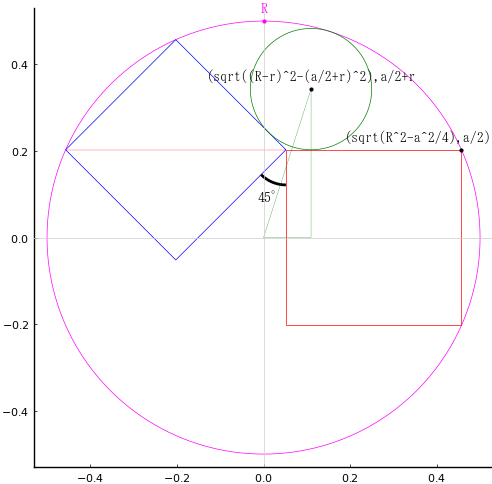
大正方形の辺が \(x-y\) 軸に並行になるように時計廻りに回転させて考える。このとき,必ず小正方形の対角線が\(x-y\) 軸に並行になり,大正方形の辺の延長線と円の交点が小正方形の頂点になる。
大正方形,小正方形の一辺の長さを \(a,\ b\)
外円の半径と中心座標を \(R,\ (0,\ 0)\)
円の半径と中心座標を \(r,\ (x,\ y)\)
とおくと,以下の関係式が成り立つ。
\( (\sqrt{2} - 1)r^2 - 2(a + b)r + \sqrt{2}a b = 0\)
この式は \(a,\ b,\ r\) を含むので,どれか 2 つの変数に実値を与えれば残りの変数の値が決定できる。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms r, a, b
eq = (√Sym(2) - 1)*r^2 - 2(a + b)r + √Sym(2)a*b ⩵ 0
\(\sqrt{2} a b + r^{2} \left(-1 + \sqrt{2}\right) - r \left(2 a + 2 b\right) = 0\)
1. \(a,\ b\) を与えて \(r\) を求める
ans_r = solve(eq, r)[1] |> factor # 1 of 2
@show(ans_r)
ans_r = (1 + sqrt(2))*(a + b - sqrt(a^2 + sqrt(2)*a*b + b^2))
\(\left(1 + \sqrt{2}\right) \left(a + b - \sqrt{a^{2} + \sqrt{2} a b + b^{2}}\right)\)
ans_r(a => 19.6, b => 24.5).evalf()
\(8.00018413855404\)
2. \(b,\ r\) を与えて \(a\) を求める
ans_a = solve(eq, a)[1]
@show(ans_a)
ans_a = r*(2*b - sqrt(2)*r + r)/(sqrt(2)*b - 2*r)
\(\displaystyle \frac{r \left(2 b - \sqrt{2} r + r\right)}{\sqrt{2} b - 2 r}\)
ans_a(b => 47.95, r => 38.36/2).evalf()
\(57.2800011343656\)
3. \(a,\ r\) を与えて \(b\) を求める
大西佐兵衛が掲出した算額の場合である。
ans_b = solve(eq, b)[1]
@show(ans_b)
ans_b = r*(2*a - sqrt(2)*r + r)/(sqrt(2)*a - 2*r)
\(\displaystyle \frac{r \left(2 a - \sqrt{2} r + r\right)}{\sqrt{2} a - 2 r}\)
ans_b(a => 11.31, r => 7.54/2).evalf()
\(9.3900083909132\)
ans_r(a => 0.405417522627599, b => 0.359715193221452).evalf() |> println
0.140086998431592
4. 外円の半径
外円の半径 \(R\) は以下の関係式において,\(a,\ b\) を与えれば求まる。
@syms R
eq2 = 2R^2 ⩵ (a^2 + √Sym(2)a*b + b^2)
\(2 R^{2} = a^{2} + \sqrt{2} a b + b^{2}\)
ans_R = solve(eq2, R)[2] # 2 of 2
@show(ans_R)
ans_R = sqrt(2)*sqrt(a^2 + sqrt(2)*a*b + b^2)/2
\(\displaystyle \frac{\sqrt{2} \sqrt{a^{2} + \sqrt{2} a b + b^{2}}}{2}\)
ans_R(a => 0.405417522627599, b => 0.359715193221452).evalf()
\(0.5\)
描画関数プログラムのソースを見る
function draw(a, b, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
plot()
R = sqrt(2)*sqrt(a^2 + sqrt(2)*a*b + b^2)/2
circle(0, 0, R, :magenta)
y1 = a/2
x1 = sqrt(R^2 -y1^2)
(x2, y2) = (x1 - a, y1)
plot!([x1, x2, x2, x1, x1], [y1, y1, -y1, -y1, y1], color=:red, lw=0.5)
(x3, y3) = (x2 - b*cos(pi/4), y2 + b*sin(pi/4))
(x4, y4) = (x3 - b*sin(pi/4), y3 - b*cos(pi/4))
(x5, y5) = (x4 + b*cos(pi/4), y4 - b*sin(pi/4))
plot!([x2, x3, x4, x5, x2], [y2, y3, y4, y5, y2], color=:blue, lw=0.5)
r = (1 + sqrt(2))*(a + b - sqrt(a^2 + sqrt(2)*a*b + b^2))
y = a/2 + r
x = sqrt( (R - r)^2 -y^2)
circle(x, y, r, :green)
length = 0.2a
circle(x2, y2, length, :black, beginangle=225, endangle=270, lw=2)
segment(x4, y4, x2, y2, :red, lw=0.2)
plot!([0, x, x, 0], [0, y, 0, 0], color=:green, lw=0.2)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x1, y1, "(sqrt(R^2-a^2/4),a/2)", :black, :right, :bottom, delta=delta, deltax=5delta)
point(x2 - 1.1length*sin(pi/8), y2 - 1.1length*cos(pi/8), "45°", :black, :center, delta=-delta, mark=false)
point(x, y, "(sqrt( (R-r)^2-(a/2+r)^2),a/2+r", :black, :center, :bottom, delta=delta)
point(0, R, "R", :magenta, :center, :bottom, delta=delta)
end
end;
draw(0.405417522627599, 0.359715193221452, true)
以下のアイコンをクリックして応援してください