埼玉県鴻巣市 薬師堂 明治23年(1890)
https://yamabukiwasan.sakura.ne.jp/ymbk351.pdf
https://yamabukiwasan.sakura.ne.jp/ymbk36.pdf
キーワード:円3個,外円,楕円,正方形
#Julia #SymPy #算額 #和算 #数学
大円の中に□ 2 個,楕円 2 個を容れる。楕円の長径が 4 寸,短径が 3 寸のとき,小円の直径はいかほどか。
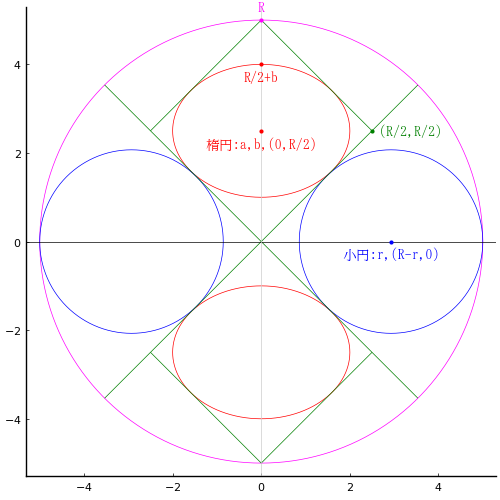
欠字が 1 個あるせいか,題意が今ひとつはっきりしない。外円の中に入っているのは小円 2 個と楕円 2 個とその楕円が内接する正方形である。
外円の半径を \(R\)
楕円の長半径,短半径を \(a,\ b\)
正方形の一辺の長さを \(s\)
小円の半径を \(r\)
とおき,以下の連立方程式を解く。
(1) 楕円が内接する正方形の一辺の長さは,算法助術の公式89 より \(4(a^2 + b^2) = 2s^2\)
(2) 外円の半径はその正方形の対角線の長さに等しい
\(R = \sqrt{2}s\)
(3) 小円がその正方形と接するので,
\(r/(R - r) = \sin(\pi/4)\)
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a, b, s, r, R
eq1 = 4(a^2 + b^2) ⩵ 2s^2
eq2 = R - sqrt(Sym(2))s
eq3 = r/(R - r) ⩵ sin(PI/4)
res = solve( (eq1, eq2, eq3), (r, R, s))[2] # 2 of 2
(2*(-1 + sqrt(2))*sqrt(a^2 + b^2), 2*sqrt(a^2 + b^2), sqrt(2*a^2 + 2*b^2))
# r
ans_r = res[1]
@show(ans_r)
ans_r = 2*(-1 + sqrt(2))*sqrt(a^2 + b^2)
\(2 \left(-1 + \sqrt{2}\right) \sqrt{a^{2} + b^{2}}\)
ans_r(a => 4//2, b => 3//2)
\(-5 + 5 \sqrt{2}\)
ans_r(a => 4//2, b => 3//2).evalf()
\(2.07106781186548\)
# 2r: 小円の直径
ans_r(a => 4//2, b => 3//2).evalf() * 2
\(4.14213562373095\)
術は小円の直径を求める式で,sqrt(17.16) としている。
マジックナンバー 17.16 は,正確には 17.1572875253810 というものであろう。
\(\sqrt{17.1572875253810}≒4.142135623730952(答の 4.142)\)
\(\sqrt{17.16}≒4.142463035441596(答の 4.142)\)
# R: 外円の半径
ans_R = res[2]
@show(ans_R)
ans_R = 2*sqrt(a^2 + b^2)
\(2 \sqrt{a^{2} + b^{2}}\)
ans_R(a => 4//2, b => 3//2).evalf()
\(5.0\)
# s: 正方形の一辺の長さ
ans_s = solve(eq1, s)[2]
@show(ans_s)
ans_s = sqrt(2*a^2 + 2*b^2)
\(\sqrt{2 a^{2} + 2 b^{2}}\)
ans_s(a => 4/2, b => 3/2)
\(3.53553390593274\)
描画関数プログラムのソースを見る
function draw(a, b, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 2*(-1 + sqrt(2))*sqrt(a^2 + b^2)
R = 2*sqrt(a^2 + b^2)
s = sqrt(2*a^2 + 2*b^2)
x = R*cos(pi/4)
plot()
circle(0, 0, R, :magenta)
ellipse(0, R/2, a, b, color=:red)
ellipse(0, -R/2, a, b, color=:red)
circle2(R - r, 0, r, :blue)
plot!([-R/2, 0, R/2], [R/2, R, R/2], color=:green, lw=0.5)
plot!([-R/2, 0, R/2], -[R/2, R, R/2], color=:green, lw=0.5)
segment(x, x, -x, -x, :green)
segment(-x, x, x, -x, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(R - r, 0, "小円:r,(R-r,0)", :blue, :center, delta=-delta)
point(0, R, "R", :magenta, :center, :bottom, delta=delta)
point(0, R/2, "楕円:a,b,(0,R/2)", :red, :center, delta=-delta)
point(0, R/2 + b, "R/2+b", :red, :center, delta=-delta)
point(R/2, R/2, " (R/2,R/2)", :green, :left, :vcenter)
end
end;
draw(4/2, 3/2, true)
以下のアイコンをクリックして応援してください