九十五 群馬県尾島町世良田 八坂神社 安政5年(1858)
群馬県和算研究会:群馬の算額,上武印刷株式会社,高崎市,1987年3月31日.
キーワード:3次元,楕円錐台
#Julia #SymPy #算額 #和算 #数学
上面が円,下面が楕円の物体がある。上面の半径,下面の長半径と短半径,高さが与えられたとき,体積を求めよ。
この物体を上方から見て等高線図を描くと,一番上は円であるがその下はすべて同心楕円である。
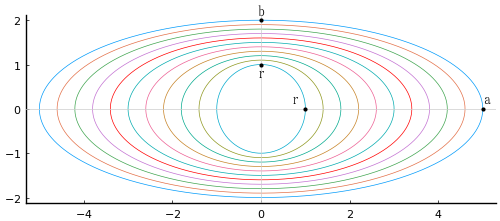
上面の半径を \(r\),下面の長半径と短半径を \(a,\ b\),高さを \(h\) とすると,高さが \(x\) で水平に切断したときの切断面は長半径 \(a_x\),短半径 \(b_x\) はそれぞれ以下のようなる。
\(a+x = a - (a - r)x/h\),\(b_x = b - (b - r)x/h\) で,面積 \(S\) は \(\pi a_x b_x\) である。
体積 \(V\) は \(S\) を 0 から h まで積分することによって得られる。
\(V = \int_{0}^{h} S dx\)
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a, b, r, h, x, ax, bx
ax = a - (a - r)*x/h
bx = b - (b - r)*x/h
V = integrate(PI*ax*bx, (x, 0, h)) |> simplify
\(\displaystyle \frac{\pi h \left(2 a b + a r + b r + 2 r^{2}\right)}{6}\)
長半径,短半径,半径,高さが 5,2,1,10 のときは 151.843644923507 である。
V(a => 5, b => 2, r => 1, h => 10).evalf()
\(151.843644923507\)
術は,( (a + b + 2r)*2r + (2a * 2b)) * h * (pi/4)/3 に相当するので,同じものである。
@syms 長径, 短径, 円径, 高さ
V2 = ( ( (長径 + 短径)/2 + 円径)*円径 + (長径 * 短径))* 高さ * (pi/4)/3;
V2(長径 => 10, 短径 => 4, 円径 => 2, 高さ => 10)
\(151.843644923507\)
描画関数プログラムのソースを見る
function draw(a, b, r, h, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
plot()
δ =(a - r)/5
c = 0
for x in 0:10
x2 = a - x*(a - r)/h
y2 = b - x*(b - r)/h
c += 1
ellipse(0, 0, x2, y2, color= c == 5 ? :red : c)
end
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a, 0, "a", :black, :left, :bottom, delta=delta)
point(r, 0, "r ", :black, :right, :bottom, delta=delta)
point(0, b, "b", :black, :center, :bottom, delta=delta)
point(0, r, "r", :black, :center, delta=-delta)
end
end;
draw(5, 2, 1, 10, true)
以下のアイコンをクリックして応援してください