埼玉県鴻巣市 薬師堂 明治23年(1890)
https://yamabukiwasan.sakura.ne.jp/ymbk351.pdf
キーワード:円4個,外円,楕円
#Julia #SymPy #算額 #和算 #数学
外円の中に楕円 3 個と小円 3 個を容れる。楕円の長径が 3 寸,短径が 2 寸のとき,外円の直径はいかほどか。
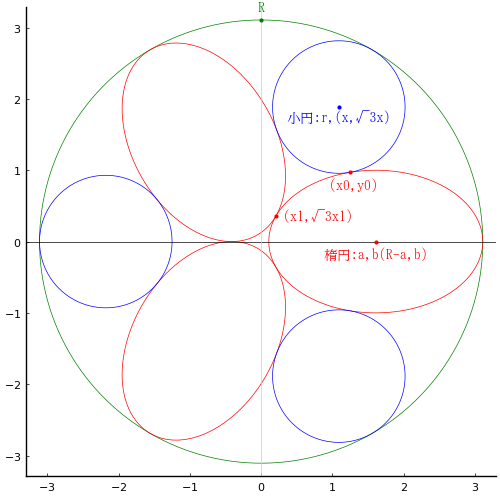
外円の直径を求めるのに,小円の情報は不要である。
楕円の長径が \(x\) 軸上に重なるように図を回転させて考える。
外円の半径と中心座標を \(R,\ (0,\ 0)\)
2 つの楕円の交点座標を \( (x_1,\ y_1); y_1 = \sqrt{3}x_1\)
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a, b, R, r, x, x1, y1, x0, y0
y1 = √Sym(3)x1
eq1 = (x1 - (R - a))^2/a^2 + y1^2/b^2 - 1
eq2 = -b^2*(x1 - (R - a))/(a^2*y1) - √Sym(3);
res = solve([eq1, eq2], (R, x1))[2]; # 2 of 2
# R: 外円の半径
ans_R = res[1]
\(\displaystyle a + \sqrt{3} \left(a^{2} + \frac{b^{2}}{3}\right) \sqrt{\frac{1}{3 a^{2} + b^{2}}}\)
小細工をして簡約化すれば,以下のようになる。
ans_R = (ans_R - a)^2 |> simplify |> x -> a + sqrt(x) |> simplify
@show(ans_R)
ans_R = a + sqrt(9*a^2 + 3*b^2)/3
\(\displaystyle a + \frac{\sqrt{9 a^{2} + 3 b^{2}}}{3}\)
楕円の長径が 3 寸,短径が 2 寸のとき,外円の直径は 6.21455025366432 である。
ans_R(a => 3/2, b => 2/2).evalf() * 2
\(6.21455025366432\)
\(a,\ b\) に「長径」,「短径」を代入すれば,円の「直径」が得られる。
ans_R(a => 3, b => 2).evalf()
\(6.21455025366432\)
術は \(\sqrt{93}/3 + 3\) であるが,これは一般解ではなく,長径 = 3,短径 = 2 のときに限ってのものである。
マジックナンバー 93 は,9*長径^2 + 3*短径^2 = 93 由来である。
最初に,「外円の直径を求めるためには小円の情報は不要」と書いたが,図を描くときには以下のようにして小円の半径と中心座標を求めればよい。
小円の半径と中心座標を \(r,\ (x, \sqrt{3}x)\)
小円と楕円の接点の座標を \( (x_0,\ y_0)\)
とおき,以下の連立方程式を解く。
@syms a, b, R, r, x, x0, y0
R = a + sqrt(9a^2 + 3b^2)/3
eq3 = (x0 - x)^2 + (y0 - √Sym(3)x)^2 - r^2
eq4 = (x0 - (R - a))^2/a^2 + y0^2/b^2 - 1
eq5 = -b^2*(x0 - (R - a))/(a^2*y0) + (x0 - x)/(y0 - √Sym(3)x)
eq5 = -b^2*(x0 - (R - a))*(y0 - √Sym(3)x) + (x0 - x)*(a^2*y0)
eq6 = x^2 + (√Sym(3)x)^2 - (R - r)^2;
function H(u)
(x, r, x0, y0) = u
return [
-r^2 + (-x + x0)^2 + (-sqrt(3)*x + y0)^2, # eq3
-1 + y0^2/b^2 + (x0 - sqrt(9*a^2 + 3*b^2)/3)^2/a^2, # eq4
a^2*y0*(-x + x0) - b^2*(x0 - sqrt(9*a^2 + 3*b^2)/3)*(-sqrt(3)*x + y0), # eq5
4*x^2 - (a - r + sqrt(9*a^2 + 3*b^2)/3)^2, # eq6
]
end;
a = 3/2
b = 1
R = a + sqrt(3)*(a^2 + b^2/3)*sqrt(1/(3*a^2 + b^2))
iniv = BigFloat[1.08874, 0.92895, 1.249, 0.9712]
res = nls(H, ini=iniv)
([1.0890798084354838, 0.9291155099611917, 1.2423237785894305, 0.9699508609353625], true)
描画関数プログラムのソースを見る
function draw(a, b, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, x1) = (a + sqrt(3)*(a^2 + b^2/3)*sqrt(1/(3*a^2 + b^2)), sqrt(3)*b^2*sqrt(1/(3*a^2 + b^2))/3)
(x, r, x0, y0) = [1.0890798084354838, 0.9291155099611917, 1.2423237785894305, 0.9699508609353625]
plot()
circle(0, 0, R, :green)
ellipse(R - a, 0, a, b, color=:red)
ellipse( (R - a)*cosd(120), (R - a)*sind(120), a, b, color=:red, φ=120)
ellipse( (R - a)*cosd(240), (R - a)*sind(240), a, b, color=:red, φ=240)
rotate(r - R, 0, r, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(R - a, 0, "楕円:a,b(R-a,b)", :red, :center, delta=-delta)
point(x, √3x, "小円:r,(x,√3x)", :blue, :center, delta=-delta/2)
point(0, R, "R", :green, :center, :bottom, delta=delta)
point(x1, √3x1, " (x1,√3x1)", :red, :left, :vcenter)
point(x0, y0, " (x0,y0)", :red, :center, delta=-delta)
end
end;
draw(3/2, 2/2, true)
以下のアイコンをクリックして応援してください