算額（その1729） - 算額あれこれ

三十四埼玉県武蔵国埼玉郡下忍村遍照院境内金毘羅社（神楽堂）天保11年(1840)

埼玉県立図書館：埼玉県史料集第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

27 岩手県一関市萩荘字八幡八幡神社弘化3年(1846)

安富有恒：和算—岩手の現存算額のすべて，青磁社，東京都，1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf

キーワード：楕円，長方形
#Julia #SymPy #算額 #和算 #数学

長方形の中に楕円を複数個容れる（図には 3 個の楕円の半径と中心座標を描く）。長方形の短辺と楕円の個数およびその長径と短径が与えられたとき，長方形の長辺を求める術を述べよ。

長方形の短辺と長辺をそのまま変数名「短辺」，「長辺」
楕円の長径と短径をそのまま変数名「長径」，「短径」
楕円の長半径と短半径を \(a\) = 長径/2, \(b\) = 短径/2
楕円の個数を \(n\)
とおく。

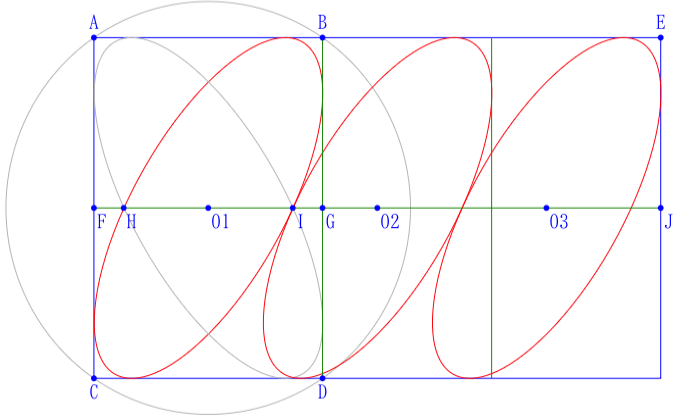
最も左側の楕円に外接する長方形 ABDC を考える。
4 つの頂点は，楕円の中心 \(O_1\) を中心とする半径 \(\sqrt{a^2 + b^2}\) の円周上にある（証明抜き）。\(BC\) はその円の直径である。
\(BC = 2\sqrt{a^2 + b^2} = 2\sqrt{(長径/2)^2 + (短径/2)^2} = \sqrt{長径^2 + 短径^2}\)
直角三角形 ABC において，
\(AB^2 + AC^2 = BC^2 = 長径^2 + 短径^2\)
\(AB^2 = 長径^2 + 短径^2 - 短辺^2\)
\(AB = \sqrt{長径^2 + 短径^2 - 短辺^2}\)

長方形 ABDC の中に描かれた赤と灰色の楕円の交点間の距離 \(HI \) は，『埼玉の算額』の 174 ページに掲載されている『三木神社の第7問』の乙斜に相当するものである。「算額（その1167）」参照。

\(\displaystyle HI = 乙斜 = \frac{長径\cdot 短径}{短辺}\)

長辺は \(AB\) と \(HI\) で以下のように表すことができる。

\(長辺 = AE = FJ = 2\cdot FH + n\cdot HI = (AB - HI) + n\cdot HI = AB + (n - 1)HI\)

すなわち，\(\displaystyle 長辺 = \sqrt{長径^2 + 短径^2 - 短辺^2} + \frac{長径\cdot 短径}{短辺}(n - 1)\) である。

描画関数プログラムのソースを見る

function draw(n, 長径, 短径, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
deltax = 3.05
短辺 = 8.88621
AB = sqrt(長径^2 + 短径^2 - 短辺^2)
delta = 長径*短径/短辺
長辺 = 長径*短径/短辺*(n - 1) + sqrt(長径^2 + 短径^2 - 短辺^2)
@printf("短辺 = %g, 長辺 = %g\n", 短辺, 長辺)
plot([0, 長辺, 長辺, 0, 0], [-短辺/2, -短辺/2, 短辺/2, 短辺/2, -短辺/2], color=:blue, lw=0.5, showaxis=false)
circle(AB/2, 0, sqrt(長径^2 + 短径^2)/2, :gray70)
ellipse(deltax, 0, 長径/2, 短径/2, φ = 60, color=:red)
ellipse(deltax, 0, 長径/2, 短径/2, φ = 120, color=:gray70)
ellipse(delta+ deltax, 0, 長径/2, 短径/2, φ = 60, color=:red)
ellipse(2delta + deltax, 0, 長径/2, 短径/2, φ = 60, color=:red)
segment(AB, 短辺/2, AB, -短辺/2, :green)
segment(AB + 長径*短径/短辺, 短辺/2, AB + 長径*短径/短辺, -短辺/2, :green)
segment(0, 0, 長辺, 0, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
#hline!([0], color=:gray80, lw=0.5)
#vline!([0], color=:gray80, lw=0.5)
point(0, 短辺/2, "A", :blue, :center, :bottom, delta=delta)
point(AB, 短辺/2, "B", :blue, :center, :bottom, delta=delta)
point(長辺, 短辺/2, "E", :blue, :center, :bottom, delta=delta)
point(AB, -短辺/2, "D", :blue, :center, delta=-delta)
point(0, -短辺/2, "C", :blue, :center, delta=-delta)
point(0, 0, "F", :blue, :left, delta=-delta, deltax=delta/2)
point(長辺, 0, "J", :blue, :left, delta=-delta, deltax=delta/2)
point(AB/2 - 長径*短径/短辺/2, 0, "H", :blue, :left, delta=-delta, deltax=delta/2)
point(AB/2, 0, "O1", :blue, :left, delta=-delta, deltax=delta/2)
point(AB/2 + 長径*短径/短辺/2, 0, "I", :blue, :left, delta=-delta, deltax=delta/2)
point(AB, 0, "G", :blue, :left, delta=-delta, deltax=delta/2)
point(AB/2 + 長径*短径/短辺, 0, "O2", :blue, :left, delta=-delta, deltax=delta/2)
point(AB/2 + 2長径*短径/短辺, 0, "O3", :blue, :left, delta=-delta, deltax=delta/2)
end
end;