算額（その1985） - 算額あれこれ

鄙理円線一致術

数学史研究（通巻200号），p.45，2009年1月〜3月
http://www.wasan.jp/sugakusipdf/200.pdf
キーワード：円8個，外円
#Julia #SymPy #算額 #和算 #数学

外円の中に甲円 1 個，乙円 2 個，丙円 2 個，丁円 2 個を容れる。外円の直径が 275 寸，甲円の直径が 75 寸のとき，乙円，丙円，丁円の直径はいかほどか。

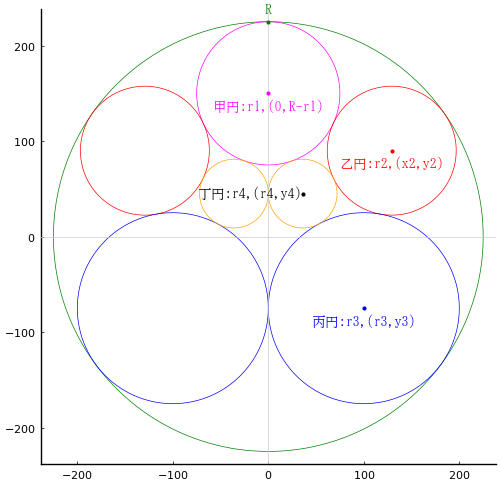
外円の半径と中心座標を \(R,\ (0,\ 0)\)
甲円の半径と中心座標を \(r_1,\ (0,\ R - r_1)\)
乙円の半径と中心座標を \(r_2,\ (x_2,\ y_2)\)
丙円の半径と中心座標を \(r_3,\ (r_3,\ y_3)\)
丁円の半径と中心座標を \(r_4,\ (r_4,\ y_4)\)
とおき，以下の連立方程式を解く。

\(R,\ r_1\) を変数のまま連立方程式を解くのは SymPy 的には無理なので，実値を与えて方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms R, r1, x2, r2, y2, r3, y3, r4, y4
@syms R::positive, r1::positive, x2::positive, r2::positive, y2::positive, r3::positive, y3::negative, r4::positive, y4::positive
R = 225
r1 = 75
eq1 = x2^2 + y2^2 - (R - r2)^2
eq2 = r3^2 + y3^2 - (R - r3)^2
eq3 = x2^2 + (R - r1 - y2)^2 - (r1 + r2)^2
eq4 = (x2 - r3)^2 + (y2 - y3)^2 - (r2 + r3)^2
eq5 = r4^2 + (R - r1 - y4)^2 - (r1 + r4)^2
eq6 = (x2 - r4)^2 + (y2 - y4)^2 - (r2 + r4)^2
eq7 = (r3 - r4)^2 + (y3 - y4)^2 - (r3 + r4)^2
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (r2, x2, y2, r3, y3, r4, y4))[1];

\(r_2 = 37800/409 - 7200\sqrt{2}/409 = 67.5248468237499\)
\(x_2 = 4500/409 + 34200\sqrt{2}/409 = 129.256977587188\)
\(y_2 = 16425/409 + 14400\sqrt{2}/409= 89.9503063525002\)
\(r_3 = 100\)
\(y_3 = -75\)
\(r_4 = 36\)
\(y_4 = 45\)

描画関数プログラムのソースを見る

function draw(R, r1, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r2, x2, y2, r3, y3, r4, y4) = (37800/409 - 7200*sqrt(2)/409, 4500/409 + 34200*sqrt(2)/409, 16425/409 + 14400*sqrt(2)/409, 100, -75, 36, 45)
println( (R, r1, r2, x2, y2, r3, y3, r4, y4))
plot()
circle(0, 0, R, :green)
circle(0, R - r1, r1, :magenta)
circle2(x2, y2, r2)
circle2(r3, y3, r3, :blue)
circle2(r4, y4, r4, :orange)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R - r1, "甲円:r1,(0,R-r1)", :magenta, :center, delta=-delta)
point(x2, y2, "乙円:r2,(x2,y2)", :red, :center, delta=-delta)
point(r3, y3, "丙円:r3,(r3,y3)", :blue, :center, delta=-delta)
point(r4, y4, "丁円:r4,(r4,y4)", :black, :right, :vcenter)
point(0, R, "R", :green, :center, :bottom, delta=delta)
end
end;
draw(225, 75, true)