17 岩手県江刺市大通り 中善観音 文政10年(1827)
安富有恒:和算—岩手の現存算額のすべて,青磁社,東京都,1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード:円7個,円弧,楕円
#Julia #SymPy #算額 #和算 #数学
円弧の中に楕円 1 個,甲円 2個,乙円 3 個,丙円 2個を容れる。甲円と乙円の直径が与えられたとき,円弧の直径を求める術を述べよ。
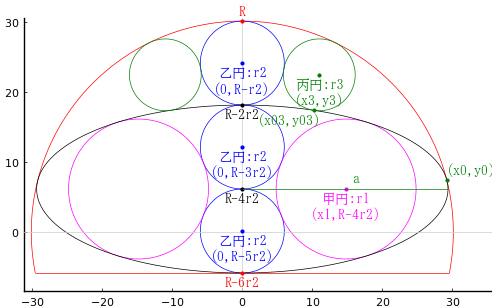
円弧の半径と中心座標を \(R, (0, R - 4r_2)\)
甲円の半径と中心座標を \(r_1, (x_1, 0)\)
乙円の半径と中心座標を \(r_2, (0, R - r_2), (0, R - 3r_2), (0, R - 5r_2)\)
丙円の半径と中心座標を\( r_3, (x_3, y_3)\)
楕円の長半径,短半径と中心座標を \(a, b, (0, R - 4r2_); b = 2r_2\)
楕円と円弧の接点座標を \( (x_0, y_0)\)
楕円と丙円の接点座標を \( (x_{03}, y_{03})\)
とおく。
丙円は円弧の直径には無関係なので,eq1〜eq6 で \(a, x_1, x_0, y_0\) を求める。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms R::positive, r1::positive, x1::positive, r2::positive, a::positive, b::positive, x0::positive, y0::negative
b = 2r2
eq1 = x1^2 + r2^2 - (r1 + r2)^2
eq2 = 4x1^2 - 4(a^2 - b^2)*(b^2 - r1^2)/b^2 # 算法助術-公式84
eq3 = x0^2/a^2 + (y0 - R + 4r2)^2/b^2 - 1 |> factor |> numerator
eq4 = -b^2*x0/(a^2*(y0 - R + 4r2)) + x0/y0 |> factor |> numerator
eq4 = R*a^2 - 4a^2*r2 - a^2*y0 + 4r2^2*y0
eq5 = x0^2 + y0^2 - R^2;
res = solve([eq1, eq2, eq4, eq5], (a, x1, x0, y0))[2]
(2*sqrt(2)*r2^(3/2)*sqrt(-1/(r1 - 2*r2)), sqrt(r1)*sqrt(r1 + 2*r2), sqrt( (R*r1 - 2*R*r2 + 8*r2^2)*(R*r1 + 2*R*r2 - 8*r2^2))/r1, -2*r2*(-R + 4*r2)/r1)
eq13 = eq3(a => res[1], x1 => res[2], x0 => res[3], y0 => res[4]) |> simplify |> numerator
eq13 |> println
4*r2^2*(R^2*r1^2 - 4*R^2*r1*r2 + 4*R^2*r2^2 + 16*R*r1*r2^2 - 32*R*r2^3 - 24*r1*r2^3 + 64*r2^4)
ans_R = solve(eq13, R)[2] # 2 of 2
ans_R |> println
2*(sqrt(6)*sqrt(r1)*r2^(3/2)*(r1 - 2*r2)^2 + 4*r2^2*(-r1^2 + 4*r1*r2 - 4*r2^2))/( (r1 - 2*r2)*(r1^2 - 4*r1*r2 + 4*r2^2))
\(\sqrt{r_1}\),\(\sqrt{r_2}\) を \(s, t\) とおき,簡約化したあとにもとに戻すと以下のようになる。
@syms s, t
ans_R = ans_R(sqrt(r1) => s, sqrt(r2) => t) |> simplify |> x -> x(s => sqrt(r1), t => sqrt(r2))
ans_R |> display
ans_R |> println
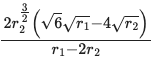
2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2)
甲円の直径が 20 寸,乙円の直径が 12 寸のとき,全円の直径は 60.3160084678767 寸である。
2*ans_R(r1 => 20/2, r2 => 12/2).evalf() |> println
60.3160084678767
術は以下のようになっており,\(2*ans_R\) と同じである。
@syms 甲径, 乙径
A = 3甲径/8乙径
全円径 = 8(1 - √A)*乙径^2/(2乙径 - 甲径)
全円径 |> display

全円径(甲径 => 20, 乙径 => 12).evalf() |> println
60.3160084678767
\(a, x_0, y_0\) は以下の通りである。
# a
res[1] |> println
res[1](r1 => 20/2, r2 => 12/2).evalf() |> println
2*sqrt(2)*r2^(3/2)*sqrt(-1/(r1 - 2*r2))
29.3938769133981
# x0
res[2] |> println
res[2](r1 => 20/2, r2 => 12/2, R => ans_R).evalf() |> println
sqrt(r1)*sqrt(r1 + 2*r2)
14.8323969741913
# y0
res[3] |> println
res[3](r1 => 20/2, r2 => 12/2, R => ans_R).evalf() |> println
sqrt( (R*r1 - 2*R*r2 + 8*r2^2)*(R*r1 + 2*R*r2 - 8*r2^2))/r1
29.2386551695722
算額の解はここまでである。
算額には丙円が描かれているが,丙円は算額の答え(全円の直径)には何の影響も与えない。
つまり,丙円は解答者を惑わす「お飾り」である。
以下は丙円を描くためのパラメータを求める連立方程式であるが,SymPy の能力的に解析解を求めることができないので,数値解を求める。
@syms R::positive, r1::positive, x1::positive, r2::positive, a::positive, b::positive, x0::positive, y0::negative,
r3::positive, x3::positive, y3::positive, x03::positive, y03::positive
b = 2r2
R = 2*r2^(Sym(3)/2)*(sqrt(Sym(6))*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2)
(a, x1, x0, y0) = (2*sqrt(Sym(2))*r2^(Sym(3)/2)*sqrt(-1/(r1 - 2*r2)), sqrt(r1)*sqrt(r1 + 2*r2),
sqrt( (R*r1 - 2*R*r2 + 8*r2^2)*(R*r1 + 2*R*r2 - 8*r2^2))/r1,
-2*r2*(-R + 4*r2)/r1);
eq6 = x3^2 + (R - r2 - y3)^2 - (r2 + r3)^2
eq7 = x3^2 + y3^2 - (R - r3)^2
eq8 = (x03 - x3)^2 + (y03 - y3)^2 - r3^2
eq9 = x03^2/a^2 + (y03 - R + 4r2)^2/b^2 - 1
eq10 = -b^2*x03/(a^2*(y03 - R + 4r2)) + (x3 - x03)/(y3 - y03);
println(eq6, ", # eq6")
println(eq7, ", # eq7")
println(eq8, ", # eq8")
println(eq9, ", # eq9")
println(eq10, ", # eq10")
x3^2 - (r2 + r3)^2 + (2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2) - r2 - y3)^2, # eq6
x3^2 + y3^2 - (2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2) - r3)^2, # eq7
-r3^2 + (x03 - x3)^2 + (y03 - y3)^2, # eq8
-1 + (-2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2) + 4*r2 + y03)^2/(4*r2^2) + x03^2*(-r1 + 2*r2)/(8*r2^3), # eq9
(-x03 + x3)/(-y03 + y3) + x03*(r1 - 2*r2)/(2*r2*(-2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2) + 4*r2 + y03)), # eq10
function H(u)
(r3, x3, y3, x03, y03) = u
return [
x3^2 - (r2 + r3)^2 + (2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2) - r2 - y3)^2, # eq6
x3^2 + y3^2 - (2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2) - r3)^2, # eq7
-r3^2 + (x03 - x3)^2 + (y03 - y3)^2, # eq8
-1 + (-2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2) + 4*r2 + y03)^2/(4*r2^2) + x03^2*(-r1 + 2*r2)/(8*r2^3), # eq9
(-x03 + x3)/(-y03 + y3) + x03*(r1 - 2*r2)/(2*r2*(-2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2) + 4*r2 + y03)), # eq10
]
end;
r1 = 10; r2 = 6
iniv = BigFloat[5, 11, 22.5, 10.2, 17.3];
res = nls(H, ini=iniv)
([5.1302159947337, 11.0029172476153, 22.47945720404743, 10.233847537564895, 17.407214314190472], true)
甲円の直径が 20 寸,乙円の直径が 12 寸のとき,丙円の半径は 5.1302159947337,中心座標は (11.0029172476153, 22.47945720404743) である。
描画関数プログラムのソースを見る
function draw(r1, r2, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = 2*r2^(3/2)*(sqrt(6)*sqrt(r1) - 4*sqrt(r2))/(r1 - 2*r2)
(a, x1, x0, y0) = (2*sqrt(2)*r2^(3/2)*sqrt(-1/(r1 - 2*r2)), sqrt(r1)*sqrt(r1 + 2*r2), sqrt( (R*r1 - 2*R*r2 + 8*r2^2)*(R*r1 + 2*R*r2 - 8*r2^2))/r1, -2*r2*(-R + 4*r2)/r1)
b = 2r2
@printf("r1 = %g; r2 = %g; R = %g; a = %g; x1 = %g; x0 = %g; y0 = %g; b = %g\n", r1, r2, R, a, x1, x0, y0, b)
y = R - 6r2
x = sqrt(R^2 - y^2)
θ = atand(y, x)
plot()
circle(0, 0, R, beginangle=θ, endangle=180 - θ, n=500)
segment(-x, y, x, y, :red)
circle(0, R - r2, r2, :blue)
circle(0, R - 3r2, r2, :blue)
circle(0, R - 5r2, r2, :blue)
circle2(x1, R - 4r2, r1, :magenta)
ellipse(0, R - 4r2, a, b)
(r3, x3, y3, x03, y03) = [5.1302159947337, 11.0029172476153, 22.47945720404743, 10.233847537564895, 17.407214314190472]
@printf("x3 = %g; y3 = %g; r3 = %g; x03 = %g; y03 = %g", x3, y3, r3, x03, y03)
circle2(x3, y3, r3, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R, "R", :red, :center, :bottom, delta=delta)
point(0, R - r2, "乙円:r2\n(0,R-r2)", :blue, :center, delta=-delta)
point(0, R - 3r2, "乙円:r2\n(0,R-3r2)", :blue, :center, delta=-delta)
point(0, R - 5r2, "乙円:r2\n(0,R-5r2)", :blue, :center, delta=-delta)
point(x1, R - 4r2, "甲円:r1\n(x1,R-4r2)", :magenta, :center, delta=-delta)
point(0, R - 2r2, "R-2r2", :black, :center, delta=-delta)
point(0, R - 4r2, "R-4r2", :black, :center, delta=-delta)
point(x0, y0, "(x0,y0)", :green, :left, :bottom, delta=delta)
point(x03, y03, "(x03,y03)", :green, :right, delta=-delta, deltax=2delta)
point(0, R - 6r2, "R-6r2", :red, :center, delta=-delta)
dimension_line(0, R - 4r2, a, R - 4r2, "a", :green, :center, :bottom, delta=delta, deltax=3delta, length=0)
point(x3, y3, "丙円:r3\n(x3,y3)", :green, :center, delta=-delta)
plot!(xlims=(-R - 2delta, R + 12delta), ylims=(R - 6r2 - 5delta, R + delta))
end
end;
draw(20/2, 12/2, true)
以下のアイコンをクリックして応援してください