算額（その1690） - 算額あれこれ

東都愛宕本地堂文化元年(1818)

八木林平質門人總州參谷郷尾高卯之助頼之
藤田嘉言(1807)：続神壁算法
http://www.wasan.jp/jinpeki/jinpeki.html
キーワード：円7個，外円，楕円
#Julia #SymPy #算額 #和算 #数学

外円内に楕円 1 個と等円 6 個を容れる。上下の 4 個の等円は楕円と外接し外円に内接する，左右の 2 個の等円は楕円と 1 点で内接する（曲率円である）。外円の直径が 19.9 寸のとき，等円の直径はいかほどか。

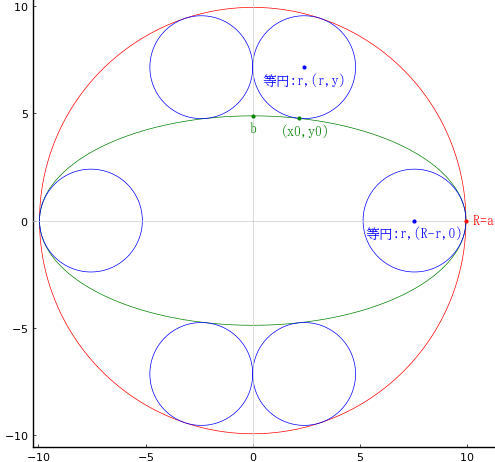
外円の半径と中心座標を \(R, (0, 0)\)
楕円の長半径，短半径と中心座標を \(a, b, (0, 0); a = R\)
等円の半径と中心座標を \(r, (r, y), (a - r, 0)\)
右上の等円と楕円の接点座標を \( (x_0, y_0)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms R::positive, a::positive, b::positive, r::positive,
y::positive, x0::positive, y0::positive
a = R
eq1 = r^2 + y^2 - (R - r)^2
eq2 = x0^2/a^2 + y0^2/b^2 - 1
eq3 = -b^2*x0/(a^2*y0) - (r - x0)/(y0 - y)
eq4 = (r - x0)^2 + (y - y0)^2 - r^2
eq5 = r - b^2/a
res = solve([eq1, eq2, eq3, eq4, eq5], (r, b, y, x0, y0))[1]

(2*R*(-3 + 2*sqrt(7))/19, R*sqrt(-114 + 76*sqrt(7))/19, R*sqrt(589 - 152*sqrt(7))/19, R*(-2 + sqrt(7))/3, 2*R*sqrt(589 - 152*sqrt(7))/57)

# r
res[1] |> println

2*R*(-3 + 2*sqrt(7))/19

等円の半径 \(r\) は，外円の半径 \(R\) の \(2(2\sqrt{7} - 3)/19\) 倍である。
外円の直径が \(19.9\) 寸のとき，等円の直径は \(19.9\cdot 2(2\sqrt{7} - 3)/19 = 4.800094966354812 寸\)である。

その他のパラメータは以下の通りである。

# b
res[2] |> println

R*sqrt(-114 + 76*sqrt(7))/19

# y
res[3] |> println

R*sqrt(589 - 152*sqrt(7))/19

# x0
res[4] |> println

R*(-2 + sqrt(7))/3

# y0
res[5] |> println

2*R*sqrt(589 - 152*sqrt(7))/57

描画関数プログラムのソースを見る

function draw(R, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 2R*(2√7 - 3)/19
b = R*sqrt(76√7 - 114)/19
y = R*sqrt(589 - 152√7)/19
x0 = R*(√7 - 2)/3
y0 = 2R*sqrt(589 - 152√7)/57
plot()
circle(0, 0, R)
ellipse(0, 0, R, b, color=:green)
circle4(r, y, r, :blue)
circle2(R - r, 0, r, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x0, y0, "(x0,y0)", :green, :left, delta=-delta, deltax=-3delta)
point(r, y, "等円:r,(r,y)", :blue, :center, delta=-delta)
point(R - r, 0, "等円:r,(R-r,0)", :blue, :center, delta=-delta)
point(R, 0, " R=a", :red, :left, :vcenter)
point(0, b, "b", :green, :center, delta=-delta)
xlims!(-R - delta, R + 5delta)
end
end;