埼玉県鴻巣市 新井稲荷神社 明治25年(1892)
https://yamabukiwasan.sakura.ne.jp/ymbk351.pdf
キーワード:円3個,直角三角形,斜線
#Julia #SymPy #算額 #和算 #数学
直角三角形の中に中鈎と斜線 1 本を設け,甲円,乙円,丙円を容れる。
股と長弦の積が 2.8,鈎と短弦の積が 5.4 のとき,丙円の直径はいかほどか。
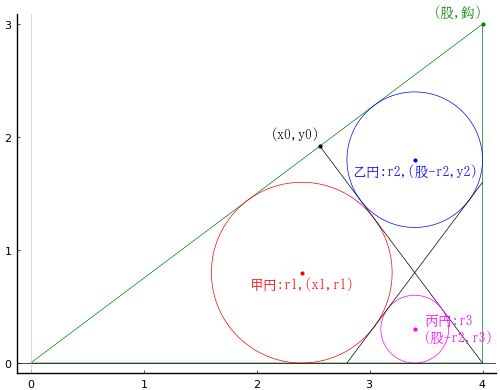
術を見ればわかるように,問は一般解を要求するものではない。\(股\cdot 長弦 = 12.8\),\(鈎\cdot 短弦 = 5.4\) の場合の解を求めよということである。
まず以下の連立方程式を解き,\(r_1,\ r_2,\ 鈎,\ 股,\ 弦,\ 長弦,\ 短弦,\ 中鈎\) を求める。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms r1, r2, r3, 鈎, 股, 弦, 長弦, 短弦, 中鈎,
K1, K2
eq1 = 股*長弦 - 12.8
eq2 = 鈎*短弦 - 5.4
eq3 = 中鈎/長弦 - 鈎/股
eq4 = 短弦/中鈎 - 鈎/股
eq5 = 鈎^2 + 股^2 - 弦^2
eq6 = 短弦 + 長弦 - 弦
eq7 = 長弦 + 中鈎 - 股 - 2r1
eq8 = 短弦 + 中鈎 - 鈎 - 2r2
eq9 = 長弦^2 + 中鈎^2 - 股^2;
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8], (r1, r2, 鈎, 股, 弦, 長弦, 短弦, 中鈎))[2] # 2 of 4
(0.800000000000000, 0.600000000000000, 3.00000000000000, 4.00000000000000, 5.00000000000000, 3.20000000000000, 1.80000000000000, 2.40000000000000)
以上の解を受け,丙円の直径を含めて図を描くために必要なパラメータをすべて求める。
なお,丙円を含む右下の直角三角形は全体の直角三角形と相似である。
(r1, r2, 鈎, 股, 弦, 長弦, 短弦, 中鈎) = (0.8, 0.6, 3.0, 4.0, 5.0, 3.2, 1.8, 2.4)
θ = atan(鈎/股)
x1 = r1/tan(θ/2)
x0 = 股 - 中鈎*sin(θ)
y0 = 中鈎*cos(θ)
y2 = 鈎 - r2/tan( (π/2 - θ)/2)
r3 = r2*tan( (pi/2 - θ)/2)
(x1, x0, y0, y2, r3)
(2.4000000000000004, 2.56, 1.92, 1.8, 0.3)
乙円の直径は 0.6 である。
描画関数プログラムのソースを見る
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, 鈎, 股, 弦, 長弦, 短弦, 中鈎) = (0.8, 0.6, 3.0, 4.0, 5.0, 3.2, 1.8, 2.4)
(x1, x0, y0, y2, r3) = (2.4, 2.56, 1.92, 1.8, 0.3)
plot([0, 股, 股, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
circle(x1, r1, r1)
segment(x0, y0, 股, 0)
circle(股 - r2, y2, r2, :blue)
circle(股 - r2, r3, r3, :magenta)
segment(股 - 2r2, 0, 股, 2r2*股/鈎)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x0, y0, "(x0,y0)", :black, :right, :bottom, delta=delta)
point(x1, r1, "甲円:r1,(x1,r1)", :red, :center, delta=-delta)
point(股 - r2, y2, "乙円:r2,(股-r2,y2)", :blue, :center, delta=-delta)
point(股 - r2, r3, "丙円:r3\n(股-r2,r3)", :magenta, :left, :vcenter, deltax=2delta)
point(股, 鈎, "(股,鈎)", :green, :right, :bottom, delta=delta)
end
end;
draw(true)
以下のアイコンをクリックして応援してください