算額（その1900） - 算額あれこれ

36 岩手県一関市真柴字境田牧沢八幡神社明治5年(1872)

安富有恒：和算—岩手の現存算額のすべて，青磁社，東京都，1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード：円3個，直角三角形，斜線
#Julia #SymPy #算額 #和算 #数学

直角三角形の中に，大円 1 個，小円 2 個と，斜（小円の共通接線）を容れる。
鈎が 3 寸，小円の直径が 1.2 寸のとき，斜はいかほどか。

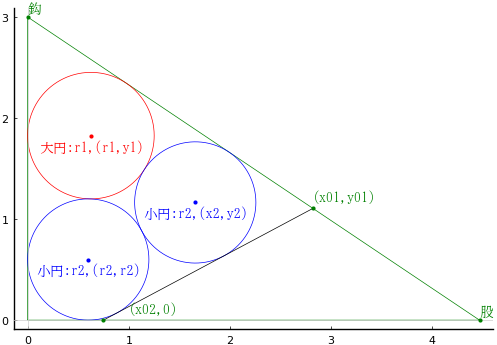
鈎，股をそのまま変数名「\(鈎\)」，「\(股\)」
大円の半径と中心座標を \(r_1, (r_1, y_1)\)
小円の半径と中心座標を \(r_2, (r_2, r_2), (x_2, y_2)\)
斜と三角形の辺の交点座標を \( (x_{01}, y_{01}), (x_{02}, 0)\)
とおき，以下の連立方程式を解き，数値解を求める。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms 鈎, 股, r1, y1, r2, x2, y2, x01, y01, x02
y1 = r2 + 2sqrt(r1*r2)
θ1 = 2atan(r2/(鈎 - r2))
θ2 = PI/2 - 2θ1
eq1 = θ2 - atan(鈎/股);
eq2 = y01/(股 - x01) - 鈎/股
eq3 = (x2 - r1)^2 + (y1 - y2)^2 - (r1 + r2)^2
eq4 = dist(x02, 0, x01, y01, x2, y2) - r2^2
eq5 = dist(x02, 0, x01, y01, r2, r2) - r2^2
eq6 = dist(0, 鈎, x01, y01, r1, r2 + 2sqrt(r1*r2)) - r1^2
eq7 = dist(0, 鈎, x01, y01, x2, y2) - r2^2;

function H(u)
(股, r1, x2, y2, x01, y01, x02) = u
return [
-4*atan(r2/(-r2 + 鈎)) - atan(鈎/股) + pi/2, # eq1
y01/(-x01 + 股) - 鈎/股, # eq2
(-r1 + x2)^2 - (r1 + r2)^2 + (r2 - y2 + 2*sqrt(r1*r2))^2, # eq3
dist(x02, 0, x01, y01, x2, y2) - r2^2, # eq4
dist(x02, 0, x01, y01, r2, r2) - r2^2, # eq5
dist(0, 鈎, x01, y01, r1, r2 + 2sqrt(r1*r2)) - r1^2, # eq6
dist(0, 鈎, x01, y01, x2, y2) - r2^2 # eq7
]
end;

鈎 = 3.0
r2 = 1.2/2
iniv = BigFloat[4.5, 0.6, 1.6, 1.1, 2.8, 1.1, 0.7]
res = nls(H, ini=iniv)

([4.472049689440994, 0.6261842099464021, 1.6588235294117648, 1.1647058823529413, 2.823529411764706, 1.1058823529411765, 0.75], true)

斜 = sqrt( (res[1][5] - res[1][7])^2 + res[1][6]^2)

2.35

「答」は 2.35 で一致する。

術は「\( (小円径^2/(2(鈎 - 小円径)) + 3鈎)/(2鈎 - 小円径) \cdot 小円径\)」である。

描画関数プログラムのソースを見る

function draw(鈎, r2, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(股, r1, x2, y2, x01, y01, x02) =
[4.472049689440994, 0.6261842099464021, 1.6588235294117648,
1.1647058823529413, 2.823529411764706, 1.1058823529411765, 0.75]
y1 = r2 + 2sqrt(r1*r2)
l = sqrt(r2^2 + (鈎 - r2)^2)
θ1 = 2atan(r2/(鈎 - r2))
θ2 = pi/2 - 2θ1
x2 = l*sin(1.5θ1)
y2 = 鈎 - l*cos(1.5θ1)
@printf("r1 = %g; x2 = %g; y2 = %g; x01 = %g; y01 = %g; x02 = %g\n", r1, x2, y2, x01, y01, x02)
plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
circle(r1, y1, r1)
circle(r2, r2, r2, :blue)
circle(x2, y2, r2, :blue)
segment(x02, 0, x01, y01)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x2, y2, "小円:r2,(x2,y2)", :blue, :center, delta=-delta)
point(r2, r2, "小円:r2,(r2,r2)", :blue, :center, delta=-delta)
point(r1, y1, "大円:r1,(r1,y1)", :red, :center, delta=-delta)
point(x01, y01, "(x01,y01)", :green, :left, :bottom, delta=delta)
point(x02, 0, "(x02,0)", :green, :left, :bottom, delta=delta, deltax=6delta)
point(股, 0, "股", :green, :left, :bottom, delta=delta/2)
point(0, 鈎, "鈎", :green, :left, :bottom, delta=delta/2)
end
end;