長野県下高井郡木島平村往郷 水穂神社 寛政12年(1800)
中村信弥「改訂増補 長野県の算額」県内の算額(P.63)
http://www.wasan.jp/zoho/zoho.html
キーワード:円2個,直角三角形,斜線
#Julia #SymPy #算額 #和算 #数学
直角三角形の中に斜線 2 本を引き,区画された領域に等円 2 個を容れる。鈎,股が与えられたとき,等円の直径はいかほどか。
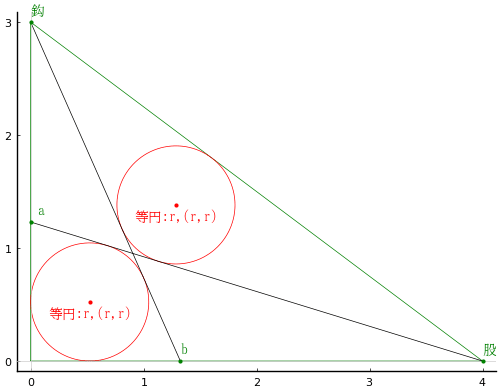
直角三角形の鈎,股,弦をそのまま変数名とする。
斜線と鈎,股の交点座標を \( (0,\ a),\ (b,\ 0)\)
等円の半径と中心座標を \(r,\ (r,\ r),\ (x,\ y)\)
とおき,以下の連立方程式を解く。
術で述べられた式は SymPy で自動的に得ることができないので,SymPy の力を借りながら手作業で方程式を解き,解を簡約化する。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms 鈎::positive, 股::positive, a::positive, b::positive,
r::positive, x::positive, y::positive
eq1 = dist2(0, a, 股, 0, r, r, r)
eq2 = dist2(0, a, 股, 0, x, y, r)
eq3 = dist2(0, 鈎, b, 0, r, r, r)
eq4 = dist2(0, 鈎, b, 0, x, y, r)
eq5 = dist2(0, 鈎, 股, 0, x, y, r);
# res = solve([eq1, eq2, eq3, eq4, eq5], (r, x, y, a, b))
eq1, eq3 を解き,\(a,\ b\) を求める。
ans_a = solve(eq1, a)[1]
ans_a |> println
2*r*(r - 股)/(2*r - 股)
ans_b = solve(eq3, b)[1]
ans_b |> println
2*r*(r - 鈎)/(2*r - 鈎)
eq2, eq4 に \(ans_a,\ ans_b\) を代入し新たな連立方程式 eq12, eq14 を解き \(x,\ y\) を求める
eq12 = eq2(a => ans_a) |> simplify |> numerator
4*r^2*(r - 股)^2*(-r^2 + x^2 - 2*x*股 + 股^2) + 4*r*y*股*(r - 股)*(2*r - 股)*(x - 股) + 股^2*(2*r - 股)^2*(-r^2 + y^2)
eq14 = eq4(b => ans_b) |> simplify |> numerator
4*r^2*(r - 鈎)^2*(-r^2 + y^2 - 2*y*鈎 + 鈎^2) + 4*r*x*鈎*(r - 鈎)*(2*r - 鈎)*(y - 鈎) + 鈎^2*(2*r - 鈎)^2*(-r^2 + x^2)
res = solve([eq12, eq14], (x, y))[2]; # 4 組の解のうちの 2 番目のものが適解
# x
ans_x = res[1] |> simplify
ans_x |> println
r*(-2*r^2 + 4*r*股 - 3*股*鈎)/(2*r^2 - 股*鈎)
# y
ans_y = res[2] |> simplify
ans_y |> println
r*(-2*r^2 + 4*r*鈎 - 3*股*鈎)/(2*r^2 - 股*鈎)
eq5 の \(x,\ y\) に res[1], res[2] を代入して新たな方程式 eq15 とする。
eq15 は因数分解でき,適解は \(4r^4 - 8r^3 股 - 8r^3 鈎 + 12r^2 股\cdot 鈎 - 4r股^2鈎 - 4r股\cdot 鈎^2 + 股^2鈎^2\) を解くことで得られる。
eq15 = eq5(x => ans_x, y => ans_y) |> simplify |> numerator
eq15 |> factor |> println
股*鈎*(2*r^2 - 2*r*股 - 2*r*鈎 + 股*鈎)*(4*r^4 - 8*r^3*股 - 8*r^3*鈎 + 12*r^2*股*鈎 - 4*r*股^2*鈎 - 4*r*股*鈎^2 + 股^2*鈎^2)
これを eq25 として \(r\) を求めると 4 個の解が得られるが,3 番目のものが適解であるが,式は異常に長いものである。
eq25 = 4*r^4 - 8*r^3*股 - 8*r^3*鈎 + 12*r^2*股*鈎 - 4*r*股^2*鈎 - 4*r*股*鈎^2 + 股^2*鈎^2
res2 = solve(eq25, r);
res2[3](鈎 => 3, 股 => 4).evalf()
0.522774424948339
eq25 の式中の \( (鈎 + 股)\),\( (鈎\cdot 股)\) を,\(\alpha,\ \beta\) に置き換え eq35 とする。
@syms α, β
eq35 = 4r^4 - 8α*r^3 + 12β*r^2 - 4α*β*r + β^2
4*r^4 - 8*r^3*α + 12*r^2*β - 4*r*α*β + β^2
res2 = solve(eq35, r);
eq35 を解いて \(r\) を求める。
res2[3]
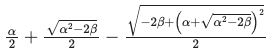
\(\alpha,\beta\) をもとに戻す。
res2[3](α => 鈎 + 股, β => 鈎*股)

最初の根号の中身は \( (鈎^2 + 股^2)\) なので,これを \(弦^2\) とする。
-2*股*鈎 + (股 + 鈎)^2 |> factor |> println
股^2 + 鈎^2
2 番目の根号の中身を因数分解して,\(\sqrt{鈎^2 + 股^2}\) を \(弦\) に置き換え,更に因数分解すると,\(2弦(股 + 鈎 + 弦)\) になる。
t = -2*股*鈎 + (股 + 鈎 + sqrt(-2*股*鈎 + (股 + 鈎)^2))^2 |> factor
2*(股^2 + 股*sqrt(股^2 + 鈎^2) + 鈎^2 + 鈎*sqrt(股^2 + 鈎^2))
@syms 弦
t(sqrt(股^2 + 鈎^2) => 弦) |> factor
2*(弦*股 + 弦*鈎 + 股^2 + 鈎^2)
以上により,等円の半径の式は以下のようになる。
ans_r = 股/2 + 鈎/2 + 弦/2 - sqrt(2弦*(股 + 鈎 + 弦))/2
更に術に合わせるために 「\(弦 + 股 + 鈎\)」を 「\(法\)」とすれば,以下のように術と同じ式になる(術は直径を求めるので,2 倍すればよい)。
@syms 法
ans_r(弦 + 股 + 鈎 => 法) |> println
弦/2 + 股/2 + 鈎/2 - sqrt(2)*sqrt(弦*法)/2
2*ans_r(鈎 => 3, 股 => 4, 弦 => 5).evalf() |> println
1.04554884989668
術は以下の通りである。
@syms 鈎, 股
弦 = sqrt(鈎^2 + 股^2)
極 = 鈎 + 股 + 弦
等円径 = 極 - sqrt(2極*弦)
等円径(鈎 => 3, 股 => 4).evalf() |> println
1.04554884989668
描画関数プログラムのソースを見る
function draw(鈎, 股, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
弦 = sqrt(鈎^2 + 股^2)
法 = 弦 + 股 + 鈎
r = 弦/2 + 股/2 + 鈎/2 - sqrt(2)*sqrt(弦*法)/2
a = 2*r*(r - 股)/(2*r - 股)
b = 2*r*(r - 鈎)/(2*r - 鈎)
x = r*(-2*r^2 + 4*r*股 - 3*股*鈎)/(2*r^2 - 股*鈎)
y = r*(-2*r^2 + 4*r*鈎 - 3*股*鈎)/(2*r^2 - 股*鈎)
plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
circle(r, r, r)
circle(x, y, r)
segment(0, a, 股, 0)
segment(0, 鈎, b, 0)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(r, r, "等円:r,(r,r)", :red, :center, delta=-delta)
point(x, y, "等円:r,(r,r)", :red, :center, delta=-delta)
point(0, 鈎, "鈎", :green, :left, :bottom, delta=delta)
point(股, 0, "股", :green, :left, :bottom, delta=delta)
point(0, a, " a", :green, :left, :bottom, delta=delta)
point(b, 0, "b", :green, :left, :bottom, delta=delta)
end
end;
draw(3, 4, true)
以下のアイコンをクリックして応援してください