29 岩手県一関市萩荘要害乙 春日神社 弘化4年(1847)
安富有恒:和算—岩手の現存算額のすべて,青磁社,東京都,1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード:円6個,外円,楕円,二等辺三角形
#Julia #SymPy #算額 #和算 #数学
全円の周上に頂点を持つ二等辺三角形の内部に,互いに外接する小円と 2 つの大円があり,図のように斜辺と底辺にも接している。
二等辺三角形の外部にある 2 つの大円は底辺に接し,2 つの楕円は斜辺に中点で接し,それぞれ全円にも内接している。
全円が楕円の短軸の端点における曲率円のとき,楕円の長軸の長さを小円の直径を用いて表せ。
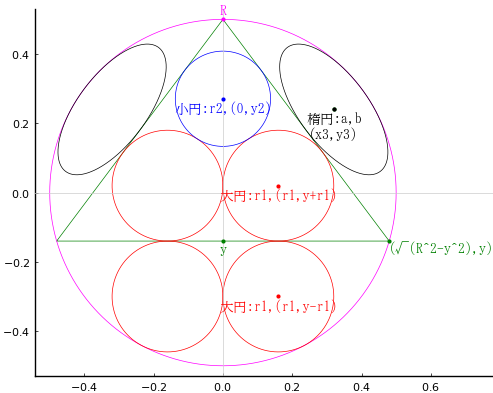
二等辺三角形の底辺と \(y\) 軸の交点座標を \( (0,\ y)\)
全円の半径と中心座標を \(R,\ (0,\ 0)\)
等円の半径と中心座標を \(r_1,\ (r_1,\ y - r_1),\ (r_1,\ y + r_1)\)
小円の半径と中心座標を \(r_2,\ (0,\ y_2)\)
とおき,以下の連立方程式を解く。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms R::positive, r1::positive, r2::positive, y2::positive, y::negative
eq1 = (r2/(R - y2))^2 - (R^2 - y^2)/( (R - y)^2 + (R^2 - y^2)) |> expand
eq2 = dist2(0, R, sqrt(R^2 - y^2) , y, r1, y + r1, r1) |> expand
eq3 = r1^2 + (y - r1)^2 - (R - r1)^2 |> expand
eq4 = r1^2 + (y2 - y - r1)^2 - (r1 + r2)^2 |> expand;
まず,eq1, eq3 を解いて \(y_2,\ y\) を求める。
res = solve([eq1, eq3], (y2, y))[1] # 1 of 4
(-sqrt(2)*sqrt(R)*r2*sqrt(sqrt(R)*sqrt(R - 2*r1) + R + r1)/(sqrt(r1)*sqrt(4*R + r1)) + R, -sqrt(R)*sqrt(R - 2*r1) + r1)
得られた \(y_2,\ y\) を eq4 に代入し eq4_2 とする。
eq4_2 = eq4(y2 => res[1], y => res[2]) |> simplify |> numerator
\(\displaystyle r_{1}^{\frac{3}{2}} \left(4 R + r_{1}\right)^{2} \left(r_{1}^{2} - 2 r_{1} r_{2} - 2 r_{1} \left(\sqrt{R} \sqrt{R - 2 r_{1}} - r_{1}\right) - r_{2}^{2} + \left(\sqrt{R} \sqrt{R - 2 r_{1}} - r_{1}\right)^{2}\right) + \sqrt{r_{1}} \left(4 R + r_{1}\right) \left(\sqrt{2} \sqrt{R} r_{2} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} - R \sqrt{r_{1}} \sqrt{4 R + r_{1}}\right)^{2} + 2 r_{1}^{2} \left(4 R + r_{1}\right)^{\frac{3}{2}} \left(\sqrt{2} \sqrt{R} r_{2} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} - R \sqrt{r_{1}} \sqrt{4 R + r_{1}}\right) - 2 r_{1} \left(4 R + r_{1}\right)^{\frac{3}{2}} \left(\sqrt{R} \sqrt{R - 2 r_{1}} - r_{1}\right) \left(\sqrt{2} \sqrt{R} r_{2} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} - R \sqrt{r_{1}} \sqrt{4 R + r_{1}}\right)\)
eq4_2 を解いて \(r_2\) を求める。
ans_r2 = solve(eq4_2, r2)[1] # 1 of 2
\(\displaystyle \frac{4 R^{\frac{5}{2}} r_{1} \sqrt{8 R^{\frac{3}{2}} \sqrt{R - 2 r_{1}} + 2 \sqrt{R} r_{1} \sqrt{R - 2 r_{1}} + 8 R^{2} + 10 R r_{1} + 2 r_{1}^{2}} - 7 R^{\frac{3}{2}} r_{1}^{2} \sqrt{8 R^{\frac{3}{2}} \sqrt{R - 2 r_{1}} + 2 \sqrt{R} r_{1} \sqrt{R - 2 r_{1}} + 8 R^{2} + 10 R r_{1} + 2 r_{1}^{2}} + 16 R^{2} r_{1}^{\frac{5}{2}} + 4 R^{2} r_{1} \sqrt{R - 2 r_{1}} \sqrt{8 R + 2 r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} + 8 R r_{1}^{\frac{7}{2}} + R r_{1}^{2} \sqrt{R - 2 r_{1}} \sqrt{8 R + 2 r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} + r_{1}^{\frac{9}{2}} - 2 r_{1}^{3} \sqrt{8 R^{\frac{5}{2}} \sqrt{R - 2 r_{1}} + 2 R^{\frac{3}{2}} r_{1} \sqrt{R - 2 r_{1}} + 8 R^{3} + 10 R^{2} r_{1} + 2 R r_{1}^{2}} - \sqrt{512 R^{\frac{11}{2}} r_{1}^{3} \sqrt{R - 2 r_{1}} + 128 \sqrt{2} R^{\frac{9}{2}} r_{1}^{\frac{7}{2}} \sqrt{4 R + r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} - 512 R^{\frac{9}{2}} r_{1}^{4} \sqrt{R - 2 r_{1}} - 160 \sqrt{2} R^{\frac{7}{2}} r_{1}^{\frac{9}{2}} \sqrt{4 R + r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} - 832 R^{\frac{7}{2}} r_{1}^{5} \sqrt{R - 2 r_{1}} - 168 \sqrt{2} R^{\frac{5}{2}} r_{1}^{\frac{11}{2}} \sqrt{4 R + r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} - 352 R^{\frac{5}{2}} r_{1}^{6} \sqrt{R - 2 r_{1}} - 46 \sqrt{2} R^{\frac{3}{2}} r_{1}^{\frac{13}{2}} \sqrt{4 R + r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} - 62 R^{\frac{3}{2}} r_{1}^{7} \sqrt{R - 2 r_{1}} - 4 \sqrt{2} \sqrt{R} r_{1}^{\frac{15}{2}} \sqrt{4 R + r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} - 4 \sqrt{R} r_{1}^{8} \sqrt{R - 2 r_{1}} + 512 R^{6} r_{1}^{3} - 1024 R^{5} r_{1}^{4} + 128 \sqrt{2} R^{4} r_{1}^{\frac{7}{2}} \sqrt{R - 2 r_{1}} \sqrt{4 R + r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} - 64 R^{4} r_{1}^{5} + 96 \sqrt{2} R^{3} r_{1}^{\frac{9}{2}} \sqrt{R - 2 r_{1}} \sqrt{4 R + r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} + 736 R^{3} r_{1}^{6} + 24 \sqrt{2} R^{2} r_{1}^{\frac{11}{2}} \sqrt{R - 2 r_{1}} \sqrt{4 R + r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} + 386 R^{2} r_{1}^{7} + 2 \sqrt{2} R r_{1}^{\frac{13}{2}} \sqrt{R - 2 r_{1}} \sqrt{4 R + r_{1}} \sqrt{\sqrt{R} \sqrt{R - 2 r_{1}} + R + r_{1}} + 74 R r_{1}^{8} + 5 r_{1}^{9}}}{\sqrt{r_{1}} \left(8 R^{\frac{5}{2}} \sqrt{R - 2 r_{1}} + 2 R^{\frac{3}{2}} r_{1} \sqrt{R - 2 r_{1}} + 8 R^{3} - 6 R^{2} r_{1} - 6 R r_{1}^{2} - r_{1}^{3}\right)}\)
得られた \(r_2\) を eq2 に代入し eq2_2 とする。
eq2_2 = eq2(r2 => ans_r2)(y2 => res[1], y => res[2]) |> simplify
\(\displaystyle 2 \sqrt{R} r_{1} \sqrt{R - 2 r_{1}} + 2 R r_{1} - r_{1}^{\frac{3}{2}} \sqrt{2 \sqrt{R} \sqrt{R - 2 r_{1}} + 2 R - r_{1}} - \frac{11 r_{1}^{2}}{2} + \frac{2 r_{1}^{\frac{5}{2}} \sqrt{2 \sqrt{R} \sqrt{R - 2 r_{1}} + 2 R - r_{1}}}{R} + \frac{3 r_{1}^{3}}{2 R} - \frac{r_{1}^{\frac{3}{2}} \sqrt{R - 2 r_{1}} \sqrt{2 \sqrt{R} \sqrt{R - 2 r_{1}} + 2 R - r_{1}}}{\sqrt{R}} - \frac{7 r_{1}^{2} \sqrt{R - 2 r_{1}}}{2 \sqrt{R}}\)
eq2_2 を解いて \(r_1\) を求める。
# r1
ans_r1 = solve(eq2_2, r1)[1]
\(\displaystyle \frac{8 R}{25}\)
得られた \(r_1\) を \(ans_{r2}\) に代入し,\(R\) だけを含む式にする。
# r2
ans_r2 = ans_r2(r1 => ans_r1) |> expand |> simplify
\(\displaystyle \frac{9 R \left(3 - \sqrt{5}\right)}{25}\)
同じく,\(r_1,\ r_2\) を res[1], res[2] に代入し,\(R\) だけを含む式 \(ans_{y2},\ ans_y\) にする。
# y2
ans_y2 = res[1](r1 => ans_r1)(r2 => ans_r2) |> simplify
\(\displaystyle \frac{R \left(-4 + 3 \sqrt{5}\right)}{5}\)
# y
ans_y = res[2](r1 => ans_r1)(r2 => ans_r2)
\(\displaystyle - \frac{7 R}{25}\)
\(R = 1\) のとき,\(r_1,\ r_2,\ y_2,\ y\) は以下のようになる。
ans_r1(R => 1).evalf() |> display
\(0.32\)
ans_r2(R => 1).evalf() |> display
\(0.275015528100076\)
ans_y2(R => 1).evalf() |> display
\(0.541640786499874\)
ans_y(R => 1).evalf() |> display
\(-0.28\)
全円の半径が 1 のとき,小円の半径は 0.275015528100076 である。
最終目的は,楕円の長径は小円の直径の何倍かを求めることである。
楕円が全円の曲率円である。このとき,二等辺三角形の斜辺を「弦」とすると,全円の「矢」は楕円の短径である。
径矢弦の定理を用い,楕円の長半径,短半径を \(a,\ b\) とおき,以下の連立方程式を解く。
@syms 矢, a, b
弦 = sqrt( (R - ans_y)^2 + (R^2 - ans_y^2))
径 = 2R
矢 = 2b
eq5 = (径/2 - 矢)^2 + (弦/2)^2 - (径/2)^2
eq6 = a^2/b - R
res2 = solve([eq5, eq6], (a, b))[3] # 3 of 4
(sqrt(5)*R/5, R/5)
全円の半径が 1 のとき,楕円の長半径,短半径は以下の通りである。
# a: 長半径
res2[1](R => 1).evalf()
\(0.447213595499958\)
# b: 短半径
res2[2](R => 1).evalf()
\(0.2\)
小円の半径は \(ans_{r_2}\) であった。比を取ると,以下のようになる。
@syms d
(p = res2[1]/ans_r2) |> x -> apart(x, d) |> factor
\(\displaystyle \frac{5 \left(5 + 3 \sqrt{5}\right)}{36}\)
p.evalf()
\(1.62613943506936\)
楕円の長半径は小円の半径 の 1.62613943506936 倍である。
術は \( (\sqrt{1125} + 25)/36 = 1.62613943506936\) 倍としており,同じである。
( (sqrt(Sym(1125)) + 25)/36).evalf()
\(1.62613943506936\)
図を描くために,楕円の中心 \( (x_3, y_3)\) から斜辺までの距離が楕円の短半径に等しいこと,および,全円の中心と楕円の中心を結ぶ線分が二等辺三角形と直交することから,\( (x_3, y_3)\) を求める。
ans_y |> simplify
\(\displaystyle - \frac{7 R}{25}\)
@syms R, x3, y3
y = -7R/25
eq7 = dist2(0, R, sqrt(R^2 - y^2), y, x3, y3, R/5)
eq8 = (R - y)/sqrt(R^2 - y^2) - x3/y3;
solve([eq7, eq8], (x3, y3))[2] # 2 of 2
(16*R^2/(25*sqrt(R^2)), 12*R/25)
描画関数プログラムのソースを見る
function draw(R, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = 8R/25
r2 = 9R*(3 - √5)/25
y2 = R*(3√5 - 4)/5
y = -7R/25
x = sqrt(R^2 - y^2)
plot([x, 0, -x, x], [y, R, y, y], color=:green, lw=0.5)
circle(0, 0, R, :magenta)
circle2(r1, y + r1, r1)
circle2(r1, y - r1, r1)
circle(0, y2, r2, :blue)
(a, b) = (√5R/5, R/5)
(x3, y3) = (16R^2/(25sqrt(R^2)), 12R/25)
ellipse(x3, y3, a, b, φ = atand(-x3/y3))
ellipse(-x3, y3, a, b, φ = 180 - atand(-x3/y3))
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x3, y3)
point(sqrt(R^2 - y^2), y, "(√(R^2-y^2),y)")
point(0, R, "R", :magenta, :center, :bottom, delta=delta/2)
point(r1, y + r1, "大円:r1,(r1,y+r1)", :red, :center, delta=-delta/2)
point(r1, y - r1, "大円:r1,(r1,y-r1)", :red, :center, delta=-delta/2)
point(0, y2, "小円:r2,(0,y2)", :blue, :center, delta=-delta/2)
point(x3, y3, "楕円:a,b\n(x3,y3)", :black, :center, delta=-delta/2)
point(0, y, "y", :green, :center, delta=-delta/2)
xlims!(-R - 3delta, R + 20delta)
end
end;
draw(1/2, true)
以下のアイコンをクリックして応援してください