算額（その1689） - 算額あれこれ

岐阜県郡上郡八幡町小野　郡上八幡神社（小野天満宮）嘉永3年(1850)

http://www.wasan.jp/gifu/gujyohatiman.html

米山忠興：算額（その11）― 郡上八幡神社 ―

https://toyo.repo.nii.ac.jp/record/2533/files/shizenkagakuhen50_089-106_OCR.pdf

上村文隆：はまぐりの数学

https://hamaguri.sakura.ne.jp/mokuzi.html
(153) 美濃・飛騨の国の和算の歴史 ― 算額の問題に挑戦しよう ―
https://hamaguri.sakura.ne.jp/minohidawasan.htm

キーワード：3次元，回転楕円体，円錐台
#Julia #SymPy #算額 #和算 #数学

円錐台の中に，短径の等しい 3 個の矮立円（回転楕円体）が入っている。円錐台の体積から矮立円の体積を差し引いた体積が最小になるときの，円錐台の下底の直径（下径）を求めよ。ただし，円錐台の上径の 3/5 と下径の 2/3 を加えると 15.41 寸とする。

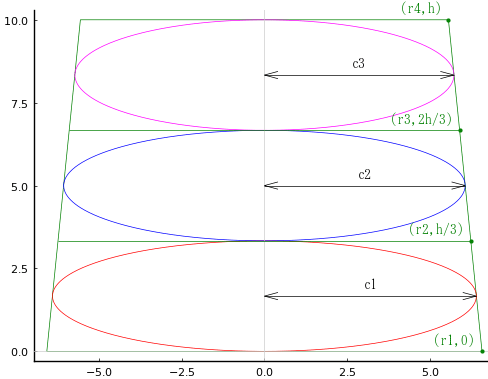
円錐台の高さを \(h\)
円錐台の上径と下径を \(r_4,\ r_1\)
円錐台を高さ h/3 で水平面で切り取ったときの切断面の半径を \(r_2,\ r_3;\ r_1 > r_2 > r_3 > r_4\)
矮立円の長径を \(c_1,\ c_2,\ c_3;\ c_1 > c_2 > c_3\)
とする。
この立体の立面図を示すと，矮立円は高さが \(h/3\) の円錐台に内接していることがわかる。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms r1::positive, r2::positive, r3::positive, r4::positive,
c1::positive, c2::positive, c3::positive, h::positive,
K::positive, V1::positive, V2::positive, V::positive;

\(r_2,\ r_3\) は \(r_1,\ r_4\) との比例関係で，以下のように表される。

r2 = 2(r1 - r4)/3 + r4
r3 = (r1 - r4)/3 + r4;

算法助術-公式82 により，台形に内接する楕円の長径は，台形の上底と下底の相乗平均であり，以下のように表される。

c1 = sqrt(r1*r2)
c2 = sqrt(r2*r3)
c3 = sqrt(r3*r4);

円錐台の体積，回転楕円体の体積（の和）をそれぞれ求め，その差の体積 \(V\) を \(r_1,\ r_4\) を含む式 eq1 で表す。
なお，\(h\) も式に含まれるが，解には関与しない。

V1 = PI*(r1^2 + r4^2 + r1*r4)*h/3 # 円錐台の体積

V2 = (4//3)PI*(c1^2 + c2^2 + c3^2)*h/6 # 回転楕円体の体積の和

eq1 = V - (V1 - V2) # 「円錐台の体積」 - 「回転楕円体の体積の和」

円錐台の上径，下径の関係式を eq2 として表す。

eq2 = 2r4*(3//5) + 2r1*(2//3) - K; # K = 15.41 # r1, r4 の関係式

eq1, eq2 を解き，\(V,\ r_4\) を求める。
\(r_4\) は算額の解としては要求されていないが，図を描くときに使われる。

res = solve([eq1, eq2], (V, r4))[1]

(pi*h*(2475*K^2 - 5250*K*r1 + 6164*r1^2)/26244, -5*(-3*K + 4*r1)/18)

「円錐台の体積」 - 「回転楕円体の体積の和」の体積は \(K,\ r_1\) および \(h\) を含む式で表される。

res[1] |> println

pi*h*(2475*K^2 - 5250*K*r1 + 6164*r1^2)/26244

\(r_1\) の二次式なので，\(r_1\) がある値をとるとき体積は最小になる。
体積が最小となるときの \(r_1\) は，「体積の導関数 = 0」を解けばよい。

f = res[1](h => 1, K => 1541//100)

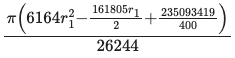
2 * solve(diff(f, r1), r1)[1] |> println
2 * solve(diff(f, r1), r1)[1].evalf() |> println

105/8
13.1250000000000

円錐台の下径が 105/8 = 13.125 のとき体積は最小値となる。

描画関数プログラムのソースを見る

function draw(r1, r4, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
h = 10 # 任意
r3 = (r1 - r4)/3 + r4
r2 = 2(r1 - r4)/3 + r4
plot([r1, r4, -r4, -r1, r1], [0, h, h, 0, 0], color=:green, lw=0.5)
r3 = (r1 - r4)/3 + r4
r2 = 2(r1 - r4)/3 + r4
c1 = sqrt(r1*r2)
c2 = sqrt(r2*r3)
c3 = sqrt(r3*r4)
ellipse(0, h/6, c1, h/6, color=:red)
ellipse(0, 3h/6, c2, h/6, color=:blue)
ellipse(0, 5h/6, c3, h/6, color=:magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(r1, 0, "(r1,0) ", :green, :right, :bottom, delta=delta)
point(r4, h, "(r4,h) ", :green, :right, :bottom, delta=delta)
point(r3, 2h/3, "(r3,2h/3) ", :green, :right, :bottom, delta=delta)
point(r2, h/3, "(r2,h/3) ", :green, :right, :bottom, delta=delta)
segment(-r2, h/3, r2, h/3, :green)
segment(-r3, 2h/3, r3, 2h/3, :green)
dimension_line(0, 5h/6, c3, 5h/6, "c3", :black, :center, :bottom, delta=delta, length=3delta)
dimension_line(0, 3h/6, c2, 3h/6, "c2", :black, :center, :bottom, delta=delta, length=3delta)
dimension_line(0, h/6, c1, h/6, "c1", :black, :center, :bottom, delta=delta, length=3delta)
end
end;