算額（その1662） - 算額あれこれ

長野県上水内郡牟飯綱町岩崎観音堂文化15年(1818)
長野県上水内郡牟礼村牟礼渋薬師堂嘉永2年(1849)
長野県下高井郡山ノ内町渋温泉医王殿慶應元年(1865)
長野県上水内郡飯綱町牟礼神社明治31年(1898)

中村信弥「改訂増補長野県の算額」県内の算額(P.99, 179, 216, 261)
http://www.wasan.jp/zoho/zoho.html
キーワード：3次元，球，回転楕円体
#Julia #SymPy #算額 #和算 #数学

算額（その1624）は 3 次元の問題として解いた

長立球（回転楕円体）の中に甲球 2 個，乙球 3 個を容れる。回転楕円体の長半径，短半径が与えられたとき，甲球の直径はいかほどか。

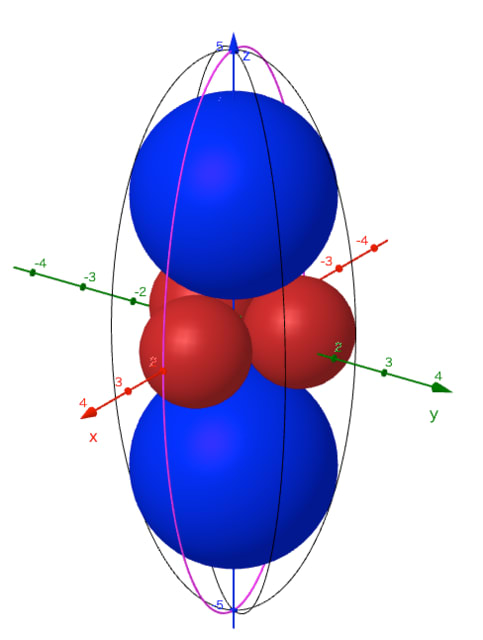
回転楕円体の長半径，短半径，中心座標を \(a,\ b,\ (0,\ 0,\ 0)\)
甲球の半径と中心座標を \(r_1,\ (0,\ 0,\ z_1)\)
乙球の半径と中心座標を \(r_2,\ (2r_2/\sqrt{3},\ 0,\ 0)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms a::positive, b::positive, r1::positive,
z1::positive, r2::positive
eq1 = z1^2 + (b - r2)^2 - (r1 + r2)^2 # 甲円と乙円が外接する
eq2 = (b - r2) -2r2/√Sym(3) # 乙円同士が外接する
eq3 = z1^2 - (a^2 - b^2)*(b^2 - r1^2)/b^2; # 算法助術-公式84

res = solve([eq1, eq2, eq3], (r1, z1, r2))[1]

(b*(4*sqrt(3)*a^2 + 7*a^2 - 4*sqrt(3)*b^2 - 6*b^2)/(a^2*(4*sqrt(3) + 7)), b*sqrt(12*a^4 + 8*sqrt(3)*a^4 - 24*a^2*b^2 - 8*sqrt(3)*a^2*b^2 + 12*b^4)/(a^2*sqrt(4*sqrt(3) + 7)), -3*b + 2*sqrt(3)*b)

# r1
res[1]

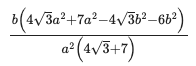
res[1](a => 10/2, b => 4/2).evalf() * 2 |> println

3.40594993262367

長径，短径が 10, 4 のとき，甲球の直径は 3.40594993262367 である。

術は小生の力では完全には読み取れないが，かなりの文字数を使っている。

中村は註で，「『術』に記された式は複雑であるが，次のように簡単になる。楕円体の長軸，短軸を a, b，甲球の直径を d とすると

\(\displaystyle d = b - \frac{2(2\sqrt{3} - 3)b^3}{a^2}\)

このことに気づいた大久保信重は，「小山氏の解とは誤りとはいえないが，迂遠である。」として，No.76 渋薬師堂に訂正算額を奉納した。大久保はNo.96 渋温泉医王殿，No.113 牟礼神社にも同問を奉納している。」と述べている。

SymPy では自動的に簡約化できないが，以下のようにして手動で分母の有理化を行うと大久保の得たのと同等の式を得る。大学入試などでは分母の有理化をしないと減点対象になるかもしれない。

まず，分子に \(4\sqrt{3} -7\) を掛ける。

num = res[1] |> numerator |> x -> x*(4sqrt(Sym(3)) - 7) |> expand

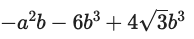
次いで，分母に同じく \(4\sqrt{3} -7\) を掛ける。

den = res[1] |> denominator |> x -> x*(4sqrt(Sym(3)) - 7) |> expand

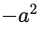
分子/分母を求める。

num/den |> simplify

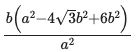
この先の細かい式変形はどうでもよいことだ。

# r2
res[3]

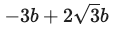
res[3](a => 10/2, b => 4/2).evalf() * 2 |> println

1.85640646055102

長径，短径が 10, 4 のとき，乙球の直径は 1.85640646055102 である。

描画関数プログラムのソースを見る

function draw(a, b, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, z1, r2) = (b*(4*sqrt(3)*a^2 + 7*a^2 - 4*sqrt(3)*b^2 - 6*b^2)/(a^2*(4*sqrt(3) + 7)), b*sqrt(12*a^4 + 8*sqrt(3)*a^4 - 24*a^2*b^2 - 8*sqrt(3)*a^2*b^2 + 12*b^4)/(a^2*sqrt(4*sqrt(3) + 7)), -3*b + 2*sqrt(3)*b)
@printf("a = %g; b = %g; r1 = %g; z1 = %g; r2 = %g\n", a, b, r1, z1, r2)
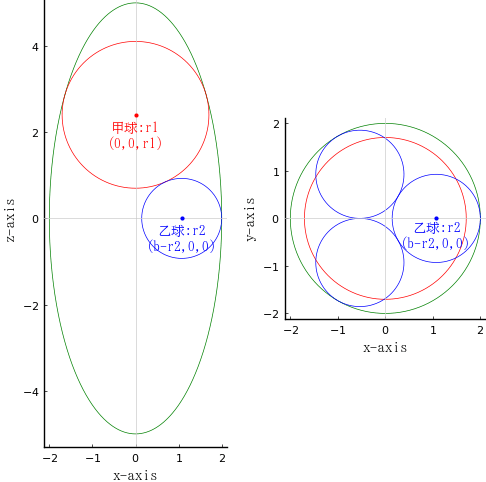
p1 = plot(xlabel="x-axis", ylabel="z-axis")
ellipse(0, 0, b, a, color=:green)
circle(0, z1, r1)
circle(b - r2, 0, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, z1, "甲球:r1\n(0,0,r1)", :red, :center, delta=-delta)
point(b - r2, 0, "乙球:r2\n(b-r2,0,0)", :blue, :center, delta=-delta)
end
p2 = plot(xlabel="x-axis", ylabel="y-axis")
circle(0, 0, b, :green)
circle(0, 0, r1)
rotate(b - r2, 0, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(b - r2, 0, "乙球:r2\n(b-r2,0,0)", :blue, :center, delta=-delta)
end
plot(p1, p2)
end;