算額（その1265） - 算額あれこれ

百二十六群馬県倉渕村水沼蓮華院明治11年(1878)

群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円3個，直角三角形，台形，斜線
#Julia #SymPy #算額 #和算 #数学

正方形を折り返した図形の中に，大円，中円，小円を容れる。大円の直径が 1.5 寸のとき，中円の直径はいかほどか。

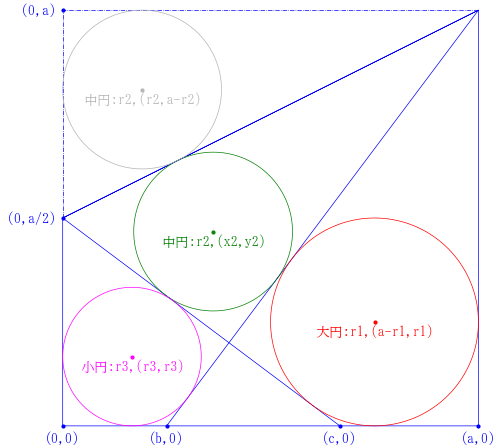
正方形の一辺の長さを \(a\) とする。「折り返した」ことによる線分の長さの関係から，大円と小円に接する斜線と正方形の一辺の交点座標 \( (0,\ a/2),\ (b,\ 0),\ (c,\ 0)\) において，b \(= a/4,\ c = 2a/3\) は事前に簡単に計算できる。
大円の半径と中心座標を \(r_1,\ (a - r_1,\ r_1)\)
中円の半径と中心座標を \(r_2,\ (x_2,\ y_2)\)
小円の半径と中心座標を \(r_3,\ (r_3,\ r_3)\)
とおき，以下の連立方程式を解く。

なお，中円の入っている直角三角形は折る前の直角三角形と合同で，その中にある（灰色で示す）中円の直径もまた簡単に計算することはできる。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms a::positive, b::positive, c::positive, r1::positive,
r2::positive, x2::positive, y2::positive, r3::positive;
b = a/4
c = 2a/3
eq1 = dist2(a/4, 0, a, a, a - r1, r1, r1)

eq2 = a + a/2 - sqrt(a^2/4 + a^2) - 2r2
eq3 = dist2(0, a/2, a, a, x2, y2, r2)
eq4 = dist2(a/4, 0, a, a, x2, y2, r2)

eq5 = dist2(a/4, 0, a, a, r3, r3, r3);

やり方は色々あるが SymPy の能力と簡便さを考慮すると，以下のように連立方程式を解くのが無難である。

res = solve([eq1, eq2, eq5, eq3, eq4], (r1, r2, r3, x2, y2))[4];

res[1] |> println
res[2] |> println
res[3] |> println

a/4
a*(3 - sqrt(5))/4
a/6

大円，中円，小円の半径は，正方形の一辺の長さの 1/4 倍，\( (3 - \sqrt{5})/4\) 倍，1/6 倍である。

中円の半径は，大円の半径の \( (3 - \sqrt{5}) = 0.7639320225002102\) 倍である。
大円の直径が 1.5 寸のとき，中円の直径は \(1.5\cdot (3 - \sqrt{5}) = 1.1458980337503153\) 寸である。

\(x_2,\ y_2\) については，簡約化できる。

a*(sqrt(5) + 5)/20
a*(25 - 7*sqrt(5))/20

描画関数プログラムのソースを見る

function draw(d1, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
a = 1 # 任意の値
b = a/4
c = 2a/3
r1 = a/4
r2 = a*(3 - √5)/4
r3 = a/6
x2 = a*(√5 + 5)/20
y2 = a*(25 - 7√5)/20
@printf("a = %g; r1 =　%g; r2 =　%g; r3 =　%g; x2 =　%g; y2 =　%g\n",
a, r1, r2, r3, x2, y2)
p = r2/r1
@printf("中円の直径は大円の直径の %g 倍である。\n", p)
@printf("大円の直径が %g のとき，中円の直径は %g である。\n", d1, d1*p)
plot([a, 0, 0], [a, a, a/2], color=:blue, lw=0.5, linestyle=:dashdot)
plot!([a, 0, 0, a, a, 0, c], [a, a/2, 0, 0, a, a/2, 0], color=:blue, lw=0.5)
segment(b, 0, a, a, :blue)
circle(a - r1, r1, r1)
circle(x2, y2, r2, :green)
circle(r3, r3, r3, :magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
# # hline!([0], color=:gray80, lw=0.5)
# # vline!([0], color=:gray80, lw=0.5)
point(a - r1, r1, "大円:r1,(a-r1,r1)", :red, :center, delta=-delta/2)
point(x2, y2, "中円:r2,(x2,y2)", :green, :center, delta=-delta/2)
circle(r2, a - r2, r2, :gray70)
point(r2, a - r2, "中円:r2,(r2,a-r2)", :gray70, :center, delta=-delta/2)
point(r3, r3, "小円:r3,(r3,r3)", :magenta, :center, delta=-delta/2)
point(0, 0, "(0,0)", :blue, :center, delta=-delta)
point(a, 0, "(a,0)", :blue, :center, delta=-delta)
point(b, 0, "(b,0)", :blue, :center, delta=-delta)
point(c, 0, "(c,0)", :blue, :center, delta=-delta)
point(0, a/2, "(0,a/2) ", :blue, :right, :vcenter)
point(0, a, "(0,a) ", :blue, :right, :vcenter)
plot!(showaxis=false, xlims=(-10delta, a + 3delta))
end
end;