28 岩手県一関市萩荘字八幡 八幡神社 弘化3年(1846)
安富有恒:和算—岩手の現存算額のすべて,青磁社,東京都,1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード:円3個,円弧,正三角形
#Julia #SymPy #算額 #和算 #数学
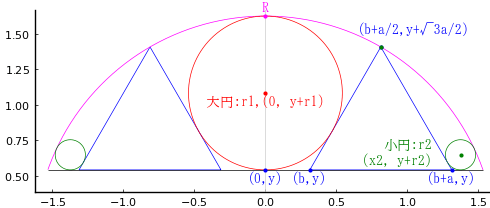
円弧(弓形)の中に,正三角形 2 個,小円 2 個,大円 1 個を容れる。正三角形の一辺の長さ,小円の直径が与えられたとき,大円の直径を求める術を述べよ。
しかし,正三角形の一辺の長さと,任意の小円の直径の両方が与えられた場合には図を描くことができない。そこで,「正三角形の一辺の長さのみが与えられる」ものとして解を求めることにする。
正三角形の一辺の長さを \(a\)
円弧の半径と中心座標を \(R, (0, 0)\)
大円の半径と中心座標を \(r_1, (0, R - r_1)\)
小円の半径と中心座標を \(r_2, (x_2, R - 2r_1 + r_2)\)
とおき,\(a\) を既知として以下の連立方程式を解き \(R, r_1, r_2, x_2\) を求める。
条件式が 4 個あるのだから,未知数は 4 個でなければならない。\(a, r_2\) が与えられてしまうと条件式が余る。使われない条件式を満たさない解になるということである。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms R, a, r1, r2, x2
y = R - 2r1
b = y/sqrt(Sym(3))
eq1 = dist(b, y, b + a/2, y + sqrt(Sym(3))*a/2, 0, R - r1) - r1^2
eq2 = dist(b + a, y, b + a/2, y + sqrt(Sym(3))*a/2, x2, y + r2) - r2^2
eq1 = dist2(b, y, b + a/2, y + sqrt(Sym(3))*a/2, 0, R - r1, r1)
eq2 = dist2(b + a, y, b + a/2, y + sqrt(Sym(3))*a/2, x2, y + r2, r2)
eq3 = x2^2 + (y + r2)^2 - (R - r2)^2
eq4 = (b + a/2)^2 + (y + sqrt(Sym(3))*a/2)^2 - R^2;
#res = solve([eq1, eq3, eq4], (R, r1, r2, x2))
res = solve([eq1, eq4], (R, r1))[4] # 4 of 4
( (-669*sqrt(3)*a^3*(-24*sqrt(3)/23 - 16/23)^2/32 + 81*sqrt(3)*a^3*(-24*sqrt(3)/23 - 16/23)/8 + 18*sqrt(3)*a^3 - 5313*sqrt(3)*a^3*(-24*sqrt(3)/23 - 16/23)^3/512)/(26*a^2), -sqrt(3)*a*(-24*sqrt(3)/23 - 16/23)/8)
# R
res[1] |> simplify |> println
3*a*(2*sqrt(3) + 9)/23
円弧の直径は,正三角形の一辺の長さの \(6(2\sqrt{3} + 9)/23\) 倍である。
# r1
res[2] |> simplify |> println
a*(2*sqrt(3) + 9)/23
大円の直径は,正三角形の一辺の長さの \(2(2\sqrt{3} + 9)/23 \)倍である。
大円の直径は,正三角形の一辺の長さのみで決定される。そして,このあと判明するが,小円の直径も正三角形の一辺の長さのみで決定される。小円の直径として任意の値を設定すると,そのような図形は描けないということになる。
引き続き,eq2, eq3 から \(x_2, r_2\) を求める。
eq12 = eq2(R => res[1], r1 => res[2]) |> simplify;
# x2
ans_x2 = solve(eq12, x2)[2] |> factor # of 2
ans_x2 |> println
(9*sqrt(3)*a + 75*a + 23*sqrt(3)*r2)/69
eq13 = eq3(R => res[1], r1 => res[2], x2 => ans_x2) |> simplify;
# r2
ans_r2 = solve(eq13, r2)[1] |> sympy.sqrtdenest |> factor # of 2
ans_r2 |> println
a*(-27 + 17*sqrt(3))/23
小円の直径は正三角形の一辺の長さの \(2(17\sqrt{3} - 27)/23\) 倍である。
なお,\(a\) を \(r_2\) で表すこともできるので,\(r_2\) を与えて \(r_1\) を求めることもできる。それは,他のパラメータと \(r_1\) の関係にも成り立つ。
eq = r2 - a*(-27 + 17*sqrt(Sym(3)))/23;
ans_a = solve(eq, a)[1] |> factor
ans_a |> println
r2*(27 + 17*sqrt(3))/6
以前求めた \(r_1\) の式中に出てくる \(a\) に \(ans_a\) を代入すれば,\(r_2\) から \(r_1\) を求める式になる。
ans_r1 = res[2](a => ans_a) |> simplify
ans_r1 |> println
r2*(5 + 3*sqrt(3))/2
ans_r1(r2 => 0.212596845971384).evalf() |> println
1.08383492305546
いずれにせよ,\(r_1\) を求めるためには,\(a\) か \(r_2\) のいずれかだけがわかればよいということである。
以上をまとめると,正三角形の一辺の長さが 1 のとき,大円,小円,円弧の直径は 1.08383492305546, 0.212596845971384, 3.25150476916637 である。
a = 1
R = 3*a*(2*sqrt(3) + 9)/23
r1 = a*(2*sqrt(3) + 9)/23
r2 = a*(-27 + 17*sqrt(3))/23
2 .*(r1, r2, R)
(1.083834923055457, 0.21259684597138379, 3.2515047691663708)
術は「\(大円直径 = (\sqrt{12}正三角形の一辺の長さ - 小円直径)/3\)」ということで,\(r_2\) に 0.1062984229856919 以外の値が与えられると成り立たない。
a = 1
r2 = 0.1062984229856919
(√12*a - 2r2)/3 |> println
1.083834923055457
描画関数プログラムのソースを見る
function draw(a, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = 3*a*(2√3 + 9)/23
r1 = a*(2√3 + 9)/23
r2 = a*(17√3 - 27)/23
x2 = (9√3*a + 75*a + 23√3*r2)/69
@printf("正三角形の一辺の長さが %g のとき,大円,小円,円弧の直径は %.15g, %.15g, %.15g である。\n", a, 2r1, 2r2, 2R)
@printf("a = %g; R = %g; r1 = %g; r2 = %g; x2 = %g\n", a, R, r1, r2, x2)
b = (R - 2r1)/√3
y = R - 2r1
x = sqrt(R^2 - y^2)
θ = atand(y, x)
plot([b, b + a, b + a/2, b], [y, y, y + √3a/2, y], color=:blue, lw=0.5)
plot!(-[b, b + a, b + a/2, b], [y, y, y + √3a/2, y], color=:blue, lw=0.5)
circle(0, 0, R, :magenta, beginangle=θ, endangle=180 - θ)
circle(0, R - r1, r1)
circle2(x2, y + r2, r2, :green)
segment(-x , y, x, y)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
ylims!(y - 10delta, R + 3delta)
point(b + a, y, "(b+a,y)", :blue, :center, delta=-delta/2)
#point(b + a/2, y, "(b+a/2,y)", :blue, :center, delta=-delta/2)
point(b + a/2, y + √3a/2, "(b+a/2,y+√3a/2)", :blue, :center, :bottom, delta=5delta, deltax=15delta)
point(b, y, "(b,y)", :blue, :center, delta=-delta/2)
point(0, y, "(0,y)", :blue, :center, delta=-delta/2)
point(0, y + r1, "大円:r1,(0, y+r1)", :red, :center, delta=-delta/2)
point(x2, y + r2, "小円:r2\n(x2, y+r2)", :green, :right, :vcenter, delta=delta, deltax=-13delta)
point(0, R, "R", :magenta, :center, :bottom, delta=delta)
point(b + a/2, y + √3a/2)
end
end;
draw(1, true)
以下のアイコンをクリックして応援してください