長野県伊那市羽広 仲仙寺 天保2年(1831)
中村信弥「改訂増補 長野県の算額」県内の算額(P.126)
http://www.wasan.jp/zoho/zoho.html
キーワード:円13個,正方形,斜線
#Julia #SymPy #算額 #和算 #数学
正方形の中に 4 本の斜線を引き各領域に等円 5 個,甲円,乙円をそれぞれ 4 個入れる。等円と乙円の径の差が与えられたとき,甲円の径を求めよ。
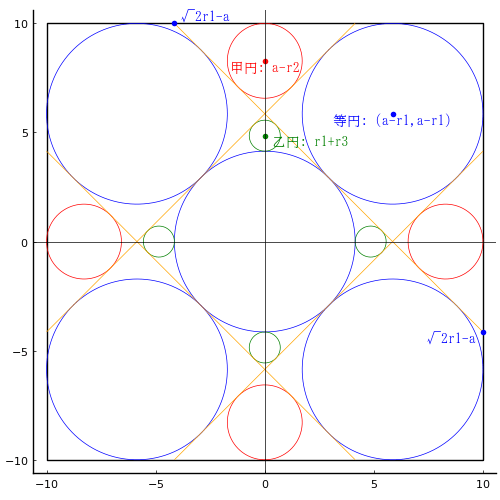
正方形の一辺の長さを \(a\)
等円,甲円,乙円の半径を \(r_1,\ r_2,\ r_3 \)
とする。
以下の 3 連立方程式を解くが,まず eq1 で \(r_1\) を \(a\) について解いて \(r_1\) とする(そうしないとあとの解が複雑になる)。以下 \(r_2,\ r_3\) も \(a\) を含む式になる。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms r1::positive, r2::positive, r3::positive, a::positive;
等円の半径 \(r_1\) を求める。
eq1 = 2(a - r1)^2 - (2r1)^2
res1 = solve(eq1, r1)[1]
r1 = res1
res1 |> println # r1
a*(-1 + sqrt(2))
甲円の半径 \(r_2\) を求める。
eq2 = distance(a, sqrt(Sym(2))r1 - a, sqrt(Sym(2))r1 - a, a, a - r2, 0) - r2^2
res2 = solve(eq2, r2)[1]
res2 |> println # r2
a*(3 - 2*sqrt(2))
乙円の半径を求める。
eq3 = distance(a, sqrt(Sym(2))r1 - a, sqrt(Sym(2))r1 - a, a, r1 + r3, 0) - r3^2
res3 = solve(eq3, r3)[1] |> sympy.sqrtdenest |> simplify
res3 |> println # r3
a*(-7 + 5*sqrt(2))
甲円の径と(等円の径 - 乙円の径)の比を求める。
res2 / (res1 - res3) |> simplify |> println # r2 / (r1 - r3)
1/2
上の式は,「甲円の径 / (等円の径 - 乙円の径) = 1 / 2」なので,「甲円の径 = (等円の径 - 乙円の径) ÷ 2」,つまり「等円と乙円の径の差の半分が甲円の径」である。
描画関数プログラムのソースを見る
function draw(a, b, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
a = 10
r1 = (√2-1)a
r2 = (3 - 2*sqrt(2))a
r3 = (5*sqrt(2) - 7)a
plot([a, a, -a, -a, a], [-a, a, a, -a, -a], color=:black, lwd=0.5)
circle(0, 0, r1, :blue)
circle4(a - r1, a - r1, r1, :blue)
circle42(0, a - r2, r2)
circle42(0, r1 + r3, r3, :green)
segment(a, √2r1 - a, √2r1 - a, a, :orange)
segment(a, a - √2r1, √2r1-a, -a, :orange)
segment(-a, √2r1-a, a - √2r1, a, :orange)
segment(-a, a - √2r1, a - √2r1, -a, :orange)
if more
point(a - r1, a - r1, "等円: (a-r1,a-r1)", :blue, :top)
point(0, a - r2, "甲円: a-r2", :red, :center)
point(0, r1 + r3, " 乙円: r1+r3 ", :green)
point(a, √2r1 - a, "√2r1-a ", :blue, :right)
point(√2r1 - a, a, " √2r1-a", :blue, :left, :bottom)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end
end;
以下のアイコンをクリックして応援してください