算額（その188） - 算額あれこれ

長野県中野市田上田上観音堂文化6年(1809)

中村信弥「改訂増補長野県の算額」県内の算額(P.86)
http://www.wasan.jp/zoho/zoho.html
キーワード：円3個，直角三角形
#Julia #SymPy #算額 #和算 #数学

第4問鈎股（直角三角形）内に大中小の 3 円を容れる。大円と中円の径を掛けると 72，大円と小円の径を掛けると 48 であるとき，それぞれの径を求めよ。
注：算額の図は「算額（その187）」と違い垂直線，水平線に接するという条件がない場合の解である。

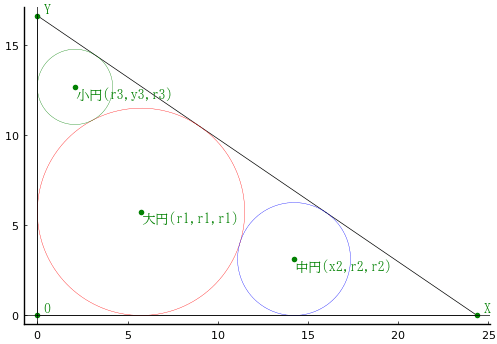
大円，中円，小円の半径を \(r_1,\ r_2,\ r_3\) とする。中円，小円の中心座標を \( (x_2,\ r_2),\ (r_3,\ y_3)\) とする。
中円，小円の中心から弦への距離，鈎股弦の面積の関係式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms X::positive, Y::positive, x2::pisitive, y3::positive,
r1::positive, r2::positive, r3::positive, l::positive;

eq1 = 2r1 * 2r2 - 72
eq2 = 2r1 * 2r3 - 48
eq3 = (x2 - r1)^2 + (r1 - r2)^2 - (r1 + r2)^2
eq4 = (r1 - r3)^2 + (y3 - r1)^2 - (r1 + r3)^2
eq5 = distance(0, Y, X, 0, r3, y3) - r3^2
eq6 = distance(0, Y, X, 0, x2, r2) - r2^2
eq7 = X^2 + Y^2 - l^2
eq8 = (X + Y + l)*r1 - X * Y;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8])

solve() では解けないので，nlsolve() を使用する。

println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
println(eq6, ",")
println(eq7, ",")
println(eq8, ",")

4*r1*r2 - 72,
4*r1*r3 - 48,
(-r1 + x2)^2 + (r1 - r2)^2 - (r1 + r2)^2,
(-r1 + y3)^2 + (r1 - r3)^2 - (r1 + r3)^2,
-r3^2 + (-X*(X*r3 + Y^2 - Y*y3)/(X^2 + Y^2) + r3)^2 + (-Y*(X^2 - X*r3 + Y*y3)/(X^2 + Y^2) + y3)^2,
-r2^2 + (-X*(X*x2 + Y^2 - Y*r2)/(X^2 + Y^2) + x2)^2 + (-Y*(X^2 - X*x2 + Y*r2)/(X^2 + Y^2) + r2)^2,
X^2 + Y^2 - l^2,
-X*Y + r1*(X + Y + l),

function H(u)
(r1, r2, r3, X, Y, l, x2, y3) = u
return [
   4*r1*r2 - 72,
   4*r1*r3 - 48,
   (-r1 + x2)^2 + (r1 - r2)^2 - (r1 + r2)^2,
   (-r1 + y3)^2 + (r1 - r3)^2 - (r1 + r3)^2,
   -r3^2 + (-X*(X*r3 + Y^2 - Y*y3)/(X^2 + Y^2) + r3)^2 + (-Y*(X^2 - X*r3 + Y*y3)/(X^2 + Y^2) + y3)^2,
   -r2^2 + (-X*(X*x2 + Y^2 - Y*r2)/(X^2 + Y^2) + x2)^2 + (-Y*(X^2 - X*x2 +    Y*r2)/(X^2 + Y^2) + r2)^2,
   X^2 + Y^2 - l^2,
   -X*Y + r1*(X + Y + l),
]
end;

iniv = [big"6.1", 4.2, 3.3, 24, 17, 31, 15, 13]
res = nls(H, ini=iniv)
println(res)

([5.748772323345361, 3.1311033012915233, 2.0874022008610154, 24.383653322069776, 16.62684846651738, 29.512957141896436, 14.234053697583931, 12.67697555362087], true)

using Printf
@printf("大円径 = %6.3f; 中円径 = %6.3f; 小円径 = %6.3f\n", 2res[1][1], 2res[1][2], 2res[1][3])

大円径 = 11.498; 中円径 = 6.262; 小円径 = 4.175

大円，中円，小円の径は元の単位で，11.498 寸，6.262 寸，4.175 寸である。

描画関数プログラムのソースを見る

function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, r3, X, Y, l, x2, y3) = res[1]
@printf("X = %6.3f; Y = %6.3f; l = %6.3f; x2 = %6.3f; y3 = %6.3f\n",
X, Y, l, x2, y3)
@printf("r1 = %6.3f; r2 = %6.3f; r3 = %6.3f\n", r1, r2, r3)
plot([0, X, 0, 0], [0, 0, Y, 0], color=:black, lw=0.5)
circle(r1, r1, r1, :red)
circle(x2, r2, r2, :blue)
circle(r3, y3, r3, :green)
if more
point(r1, r1, "大円(r1,r1,r1)")
point(x2, r2, "中円(x2,r2,r2)")
point(r3, y3, "小円(r3,y3,r3)")
point(0, 0, " O", :green, :left, :bottom)
point(X, 0, " X", :green, :left, :bottom)
point(0, Y, " Y", :green, :left, :bottom)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end
end;