算額（その187） - 算額あれこれ

長野県中野市田上田上観音堂文化6年(1809)

中村信弥「改訂増補長野県の算額」県内の算額(P.86)
http://www.wasan.jp/zoho/zoho.html
キーワード：円3個，直角三角形
#Julia #SymPy #算額 #和算 #数学

第4問鈎股（直角三角形）内に大中小の 3 円を容れる。3 円はそれぞれ鈎股弦に接し，鈎股弦内の垂直線，水平線にも接している。大円と中円の径を掛けると 72，大円と小円の径を掛けると 48 であるとき，それぞれの径を求めよ。
注：算額の図は垂直線，水平線に接するという条件がない図（「算額（その188）」参照）になっているが，答えはその図と異なり上述の問いの場合の答えになっている。

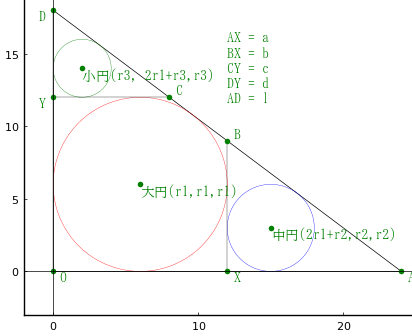
大円，中円，小円の半径を \(r_1,\ r_2,\ r_3\) とする。AX = \(a\), BX = \(b\), CY = \(c\), DY = \(d\) とする。
⊿AOD, ⊿AXB, ⊿CYD は相似で，相似比が \(r_1:r_2:r_3\) である。
また，AD^2 = l^2 = AO^2 + DO^2, 直角三角形の面積の関係について方程式を立てて解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms a::positive, b::positive, c::positive, d::positive,
r1::positive, r2::positive, r3::positive, l::positive;

eq1 = 2r1 * 2r2 - 72
eq2 = 2r1 * 2r3 - 48
eq3 = d/b - c/a
eq4 = d/b - r3/r2
eq5 = d/(d + 2r1) - c/(a + 2r1)
eq6 = d/(d + 2r1) - r3/r1
eq7 = b/(d + 2r1) - r2/r1
eq8 = (d + 2r1)^2 + (a + 2r1)^2 - l^2
eq9 = (d + 2r1 + a + 2r1 + l)*r1 - (d +2r1) * (a + 2r1)
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9],
(a, b, c, d, r1, r2, r3, l))[1]

(12, 9, 8, 6, 6, 3, 2, 30)

大円，中円，小円の半径は 6, 3, 2 で，元の単位でいえば直径 12 寸, 6 寸, 4 寸である。

描画関数プログラムのソースを見る

function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(a, b, c, d, r1, r2, r3, l) = res[1]
@printf("a = %6.3f; b = %6.3f; c = %6.3f; d = %6.3f\n", a, b, c, d)
@printf("r1 = %6.3f; r2 = %6.3f; r3 = %6.3f\n", r1, r2, r3)
plot([0, a + 2r1, 0, 0], [0, 0, d + 2r1, 0], color=:black, lw=0.5)
circle(r1, r1, r1, :red)
circle(2r1 + r2, r2, r2, :blue)
circle(r3, 2r1 + r3, r3, :green)
segment(0, 2r1, c, 2r1, :black, linewidth=0.25)
segment(2r1, 0, 2r1, b, :black, linewidth=0.25)
if more
point(0, 0, " O")
point(2r1, 0, " X")
point(2r1+a, 0, " A")
point(2r1, b, " B", :green, :left, :bottom)
point(c, 2r1, " C", :green, :left, :bottom)
point(0, 2r1, "Y ", :green, :right)
point(0, 2r1+d, "D ", :green, :right)
point(r1, r1, "大円(r1,r1,r1)")
point(2r1+r2, r2, "中円(2r1+r2,r2,r2)")
point(r3, 2r1+r3, "小円(r3, 2r1+r3,r3)")
annotate!(2r1, 2r1+r3, text("AX = a\nBX = b\nCY = c\nDY = d\nAD = l", 10, :left, :green))
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
end
end;