算額（その15） - 算額あれこれ

72 岩手県川崎村薄衣字諏訪前（現一関市川崎町）浪分神社文久年間？
88 岩手県陸前高田市気仙町字町裏諏訪神社慶應4年(1868)

安富有恒：和算—岩手の現存算額のすべて，青磁社，東京都，1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf

岩手県東磐井郡川崎村浪分神社年代不詳（文久か）

http://www.wasan.jp/iwate/namiwake5.html

岩手県陸前高田市気仙町今泉諏訪神社慶應 4 年

http://www.wasan.jp/iwate/suwa.html

キーワード：円8個，外円
#Julia #SymPy #算額 #和算 #数学

下図のように，半径 1 の円の中に 2 種類の円がありそれぞれ接している。それぞれの円の半径を求めよ。

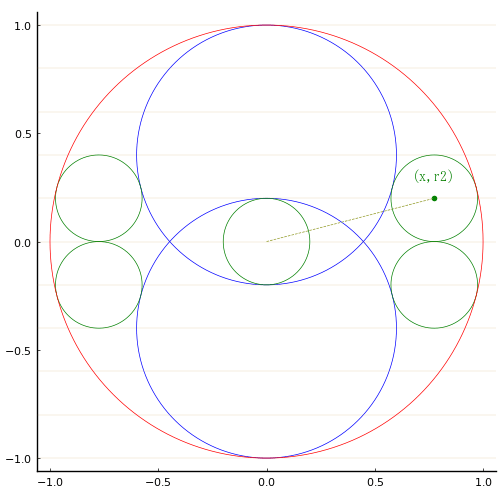
紙と鉛筆でも求めることができる。

小さい円の半径は \(r_2 = 1/5\) ，大きい円の半径は \(r_1 = 3r_2\) である。

右の小さい円の中心を \( (x,\ \pm r_2)\) とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms x::positive;

r2 = 1//5
r1 = 3r2
eq1 = x^2 + r2^2 - (1 - r2)^2
eq1 |> expand |> println

x^2 - 3/5

# x
solve(eq1, x)[1] |> println

sqrt(15)/5

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
x = sqrt(15)/5
r2 = 1/5
r1 = 3r2
@printf("r2 = %g, x = %g\n", r2, x)
plot()
circle2(0, 2r2, 3r2, :blue)
circle4( x, r2, r2, :green)
circle( 0, 0, r2, :green)
if more
hline!(-1:r2:1, linewidth=0.1)
point(x, r2, "(x,r2)\n", :green, :center, :bottom)
plot!([0, x], [0, r2], linewidth=0.5, linestyle=:dash)
end
circle(0, 0, 1)
end;