長野県長野市元善町 善光寺 寛政8年(1796)
中村信弥「改訂増補 長野県の算額」県内の算額(P.52)
http://www.wasan.jp/zoho/zoho.html
キーワード:円6個
#Julia #SymPy #算額 #和算 #数学
3 個の等円が輪違いになっており,隙間に天円,地円,人円を容れる。等円の直径が与えられたとき,天円,地円,人円の直径を与える 3 次式を求めよ。
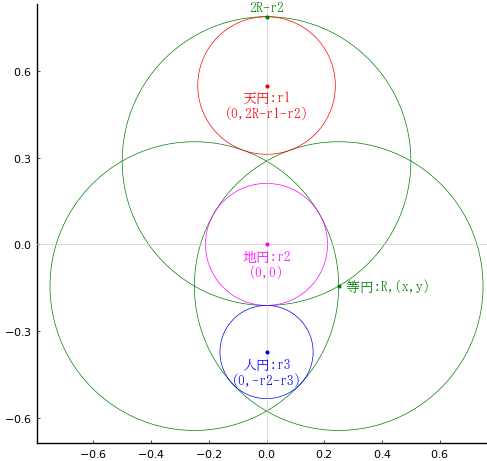
明記されてはいないが,等円の中心は他の 2 円の周上にある。
3 次方程式を求めよというのは虚仮威しで,本質的なものではない。
天円,地円,人円の直径を求めて終わりというのが潔い。
等円の半径と中心座標を \(R,\ (0,\ 2R - r_1 - r_2),\ (R/2,\ -R/2\sqrt{3})\)
天円の半径と中心座標を \(r_1,\ (0, 2R - r_2 - r_1)\)
地円の半径と中心座標を \(r_2,\ (0, 0)\)
人円の半径と中心座標を \(r_3,\ (0, -r_2 - r_3)\)
とおき,以下の連立方程式を解く。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms R::positive, x, y::negative, r1::positive, r2::positive, r3::positive
x = R/2
y = -R/2√Sym(3)
eq1 = x^2 + (2R - r1 - r2 - y)^2 - (R + r1)^2
eq2 = x^2 + y^2 - (R - r2)^2
eq3 = x^2 + (y + r2 + r3)^2 - (R - r3)^2
res = solve([eq1, eq2, eq3], (r1, r2, r3))[2];
# r1: 天円の半径
ans_r1 = res[1] |> sympy.sqrtdenest |> simplify
@show(ans_r1)
ans_r1 = R*(1 + 3*sqrt(3))/13
\(\displaystyle \frac{R \left(1 + 3 \sqrt{3}\right)}{13}\)
# 等円の半径が 1/2 のときの天円の半径
ans_r1(R => 1/2).evalf()
\(0.238313554719486\)
# r2: 地円の半径
ans_r2 = res[2] |> sympy.sqrtdenest |> simplify
@show(ans_r2)
ans_r2 = R*(3 - sqrt(3))/3
\(\displaystyle \frac{R \left(3 - \sqrt{3}\right)}{3}\)
# 等円の半径が 1/2 のときの地円の半径
ans_r2(R => 1/2).evalf()
\(0.211324865405187\)
# r3: 人円の半径
ans_r3 = res[3] |> sympy.sqrtdenest |> simplify
@show(ans_r3)
ans_r3 = -R/13 + 3*sqrt(3)*R/13
\(\displaystyle - \frac{R}{13} + \frac{3 \sqrt{3} R}{13}\)
# 等円の半径が 1/2 のときの人円の半径
ans_r3(R => 1/2).evalf()
\(0.161390477796409\)
\(ans_{r1},\ ans_{r2},\ ans_{r3}\) を解として持つ 3 次方程式は,解と係数の関係を使って構成してもよいが,以下の式を展開して作るほうが間違いがない。
@syms x
f = 39(x - ans_r1)*(x - ans_r2)*(x - ans_r3) |> expand
\(- 6 R^{3} + 2 \sqrt{3} R^{3} - 12 R^{2} x + 18 \sqrt{3} R^{2} x - 39 R x^{2} - 5 \sqrt{3} R x^{2} + 39 x^{3}\)
\(x\) の各次数の係数を取り出したいときは .coeff() を使う。
# x^3 の係数
f.coeff(x, 3)
\(39\)
# x^2 の係数
f.coeff(x, 2)
\(- 39 R - 5 \sqrt{3} R\)
# x の係数
f.coeff(x, 1)
\(- 12 R^{2} + 18 \sqrt{3} R^{2}\)
# 定数項
f.coeff(x, 0)
\(- 6 R^{3} + 2 \sqrt{3} R^{3}\)
\(R\) を特定の値にして,3 次方程式を解いてみる。
\(R = 1/2\) のとき,以下のようになる。
f(R => 1/2)
\(39 x^{3} - 19.5 x^{2} - 2.5 \sqrt{3} x^{2} - 3.0 x + 4.5 \sqrt{3} x - 0.75 + 0.25 \sqrt{3}\)
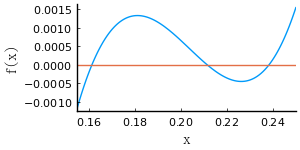
図を描いてみると,0.15 〜 0.25 の範囲に 3 個の解があることが確認できる。
using LaTeXStrings
pyplot(size=(300, 150), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(f(R => 1/2), xlims=(0.155, 0.25), xlabel=L"x", ylabel=L"f(x)")
hline!([0])
solve() で解くと正確な解が求められるが,数値演算の誤差により,虚数部が限りなく 0 に近いものとして表示されることがある。
res = solve(f(R => 1/2), x);
res[1].evalf() |> display
res[2].evalf() |> display
res[3].evalf() |> display
\(0.161390477796409 + 2.06795153138257 \cdot 10^{-25} i\)
\(0.211324865405187 - 4.13590306276514 \cdot 10^{-25} i\)
\(0.238313554719486 + 1.05879118406788 \cdot 10^{-22} i\)
find_zero では数値解を求めるので,上のような紛らわしい表示に惑わせられることがない。
using Roots
find_zero(f(R => 1/2), (0.16, 0.17)) |> println
find_zero(f(R => 1/2), (0.21, 0.22)) |> println
find_zero(f(R => 1/2), (0.23, 0.24)) |> println
0.16139047779640933
0.21132486540518441
0.23831355471948984
描画関数プログラムのソースを見る
function draw(R, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(x, y) = (R/2, -R/2√3)
(r1, r2, r3) = (0.238313554719486, 0.211324865405187, 0.161390477796409)
plot()
rotate(0, R - r2, R, :green)
circle(0, 2R - r1 - r2, r1)
circle(0, 0, r2, :magenta)
circle(0, -r2 - r3, r3, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, 2R - r1 - r2, "天円:r1\n(0,2R-r1-r2)", :red, :center, delta=-delta)
point(0, 0, "地円:r2\n(0,0)", :magenta, :center, delta=-delta)
point(0, −r2 - r3, "人円:r3\n(0,-r2-r3)", :blue, :center, delta=-delta)
point(x, y, " 等円:R,(x,y)", :green, :left, :vcenter)
point(0, 2R - r2, "2R-r2", :green, :center, :bottom, delta=delta/2)
end
end;
draw(1/2, true)
以下のアイコンをクリックして応援してください