岐阜県垂井町宮代 南宮大社 弘化2年(1845)
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF
二十六 群馬県安中市簗瀬 稲荷神社 文化11年(1814)
五十一 群馬県安中市簗瀬 稲荷神社 文政11年(1828)
群馬県和算研究会:群馬の算額,上武印刷株式会社,高崎市,1987年3月31日.
キーワード:3次元,球,回転楕円体
#Julia #SymPy #算額 #和算 #数学
矮立円(楕円を短軸を中心として回転してできる回転楕円体)の中央に赤球を容れ,赤球に外接し回転楕円体に2点で内接し互いに外接し合う萠黄球を容れる。
長径と短径が与えられたとき,萠黄球の個数を求める術を述べよ。
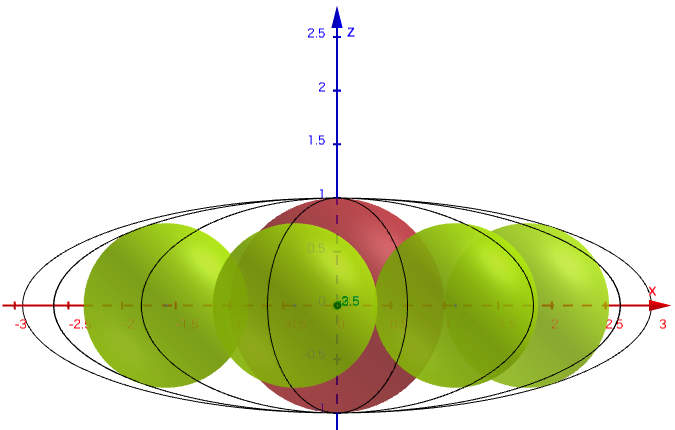
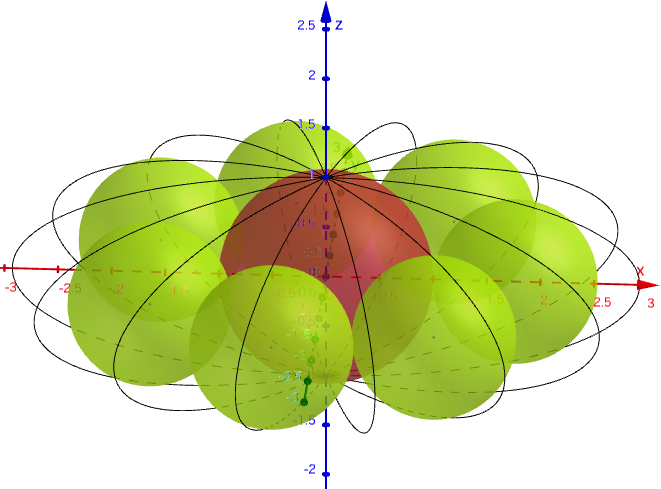
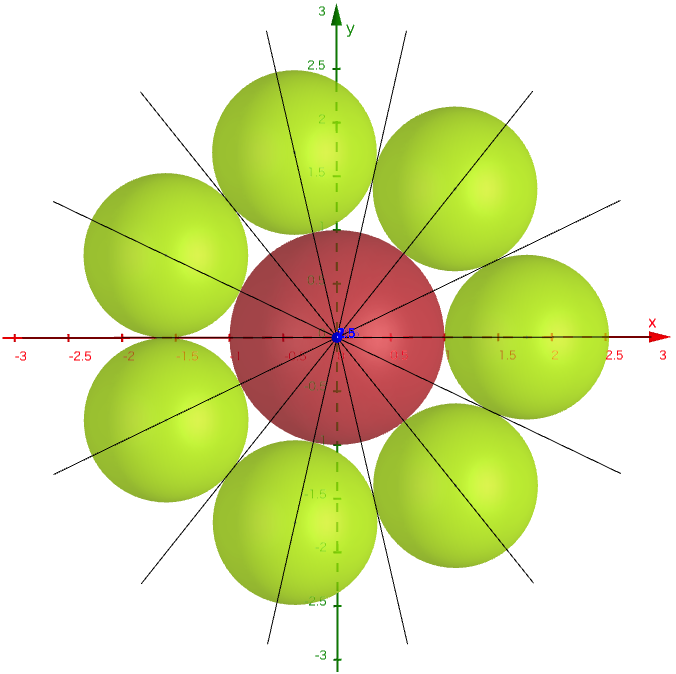
算額の問では,「楕円の長径と短径を知って,萠黄球の個数を求めよ」となっている。
しかし,長径と短径が任意の回転楕円体において「赤球に外接し回転楕円体に2点で内接し互いに外接し合う萠黄球」を容れることはできない。できるだけ詰め込んでも隙間ができる。隙間ができずに,萠黄球がすべて外接し合うためには長径がいかほどかという問いであれば,答えることができる。
回転楕円体の元になる楕円の長半径,短半径と中心座標を \(a,\ b,\ (0,\ 0)\)
赤球の半径と中心座標を \(r_1,\ (0,\ 0,\ 0);\ r_1 = b\)
中心が \(x\) 座標軸上にある萠黄球の半径と中心座標を \(r_2,\ (x_2,\ 0,\ 0) \)
とおく。
赤球の赤道上に(中心が \(x-y\) 平面にある)\(n\) 個の萠黄球を隙間なく並べることを考える。
萠黄球の半径は \(r_2 = (r_1 + r_2) \sin(180°/n)\) でなければならない。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a::positive, b::positive, r1::positive, r2::positive, n::positive
r1 = b
eq1 = (r1 + r2)*sind(180/n) ⩵ r2;
次に,算法助術の公式84から,\(y\) 軸の負の方から正の方向を眺めたとき,楕円の長半径,短半径と赤球,萠黄球の半径に以下の関係式が成り立たなければならない。
蛇足であるが,萠黄球の個数が奇数のときは左側の萠黄級はこの位置には見えないが,左の位置に萠黄球が見えるように回転させた場合を考えればよい。
\(\displaystyle (2(r_1 + r_2))^2 = \frac{4(a^2 - b^2)(b^2 - r_2^2)}{b^2}\)
# 算法助術-公式84
eq2 = (2(r1 + r2))^2 - 4(a^2 - b^2)*(b^2 - r2^2)/b^2
\(\displaystyle \left(2 b + 2 r_{2}\right)^{2} - \frac{\left(4 a^{2} - 4 b^{2}\right) \left(b^{2} - r_{2}^{2}\right)}{b^{2}}\)
2 つの条件をともに満たすときの,萠黄球の半径と楕円の長半径は連立方程式を解けば得られる。
その正確な推論過程は後半に示す。
1. 簡単な方法
条件を満たす正確な長径,短径が与えられたとき,eq2 から,萠黄球の半径 \(r_2\) を求める。
ans_r2 = solve(eq2, r2)[1]
\(\displaystyle b - \frac{2 b^{3}}{a^{2}}\)
eq1 の \(r_2\) に上の解を代入した方程式 eq11 を解いて \(n\) を求める。
eq11 = eq1(r2 => ans_r2)
\(\displaystyle \left(2 b - \frac{2 b^{3}}{a^{2}}\right) \sin{\left(\frac{\pi}{n} \right)} = b - \frac{2 b^{3}}{a^{2}}\)
\(a, b\) が与えられたとき,萠黄球の個数は以下の式で求めることができる。
ans_n = solve(eq11, n)[2] # 2 of 2
\(\displaystyle \frac{\pi}{\operatorname{asin}{\left(\frac{a^{2} - 2 b^{2}}{2 \left(a - b\right) \left(a + b\right)} \right)}}\)
\(b = 1\) に固定したとき,\(a = 2.92616406389355,\ 2.29389900113228,\ 2.04082347618428\) の 3 通りがある。
これ以外の数値の場合は,条件を満たす空間図形はない。
ans_n(a => 2.92616406389355, b => 1).evalf() |> println
ans_n(a => 2.29389900113228, b => 1).evalf() |> println
ans_n(a => 2.04082347618428, b => 1).evalf() |> println
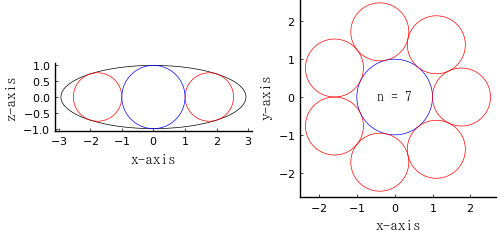
7.00000000000000
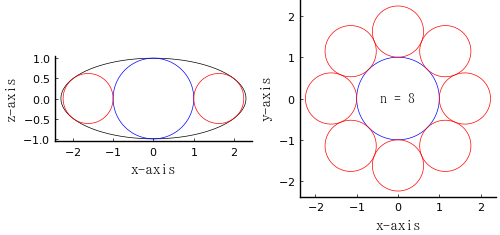
8.00000000000000
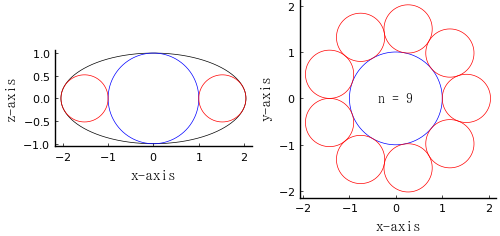
9.00000000000001
\(\verb;|;x\verb;|; < 1\)のとき,\(\arcsin(x) ≒ x\) なので,\(ans_n\) は以下の式で近似できる。計算結果の整数部分をとればよい。
\(\displaystyle \frac{\pi}{\frac{(a^2 - 2*b^2)}{(2(a^2 - b^2)}}\)
# 近似式を関数化する
approx_n(a, b) = (pi/( (a^2 - 2*b^2)/(2*(a^2 - b^2))));
# 適用してみる
approx_n(2.92616406389355, 1) |> println
approx_n(2.29389900113228, 1) |> println
approx_n(2.04082347618428, 1) |> println
7.240632386867574
8.209377223816244
9.185402424085874
整数部を取ると,\(n = 7,\ 8,\ 9\) と正しい結果が得られる。これ以外の解はない。
# a を小数点以下 2 桁で四捨五入した結果を使ってみる
approx_n(2.9, 1) |> println
approx_n(2.3, 1) |> println
approx_n(2.0, 1) |> println
7.263401423744265
8.192968075319278
9.42477796076938
同じ結果が得られる。
2. 連立方程式を解くやや精密な推論過程
res = solve( (eq1, eq2), (r2, a))[2] # 2 of 2
(-b*sin(pi/n)/(sin(pi/n) - 1), sqrt(2)*b*sqrt( (sin(pi/n) - 1)/(2*sin(pi/n) - 1)))
# r2 萠黄球の半径
@show(res[1])
res[1] = -b*sin(pi/n)/(sin(pi/n) - 1)
\(\displaystyle - \frac{b \sin{\left(\frac{\pi}{n} \right)}}{\sin{\left(\frac{\pi}{n} \right)} - 1}\)
# a 楕円の長半径
@show(res[2])
res[2] = sqrt(2)*b*sqrt( (sin(pi/n) - 1)/(2*sin(pi/n) - 1))
\(\displaystyle \sqrt{2} b \sqrt{\frac{\sin{\left(\frac{\pi}{n} \right)} - 1}{2 \sin{\left(\frac{\pi}{n} \right)} - 1}}\)
長半径の式中の \(\frac{\sin(\pi/n) - 1}{2\sin(\pi/n) - 1}\) は,\(3 ≦ n ≦ 5\) のときは負になるので,平方根がとれないので,いずれにせよ不適切解である。
\(n = 6\) のときは,赤球と萠黄球の半径が等しくなり,回転楕円体が存在しない。
題意を満たすためには,萠黄球の半径 < 赤球の半径でなければならない。
\(n = 7,\ 8,\ 9\) のときは,以下のようになり解があり得る。
題意を満たすためには,萠黄球の半径は曲率円の半径より大きくなければならない。
\(r_1 = b = 1;\ n = 7;\ r_2 = 0.766422;\ a = 2.92616\)
\(a = 2.92616,\ b = 1\) のときの曲率円の半径 = 0.341744
\(r_1 = b = 1;\ n = 8; r_2 = 0.619914;\ a = 2.2939\)
\(a = 2.2939,\ b = 1\) のときの曲率円の半径 = 0.435939
\(r_1 = b = 1;\ n = 9;\ r_2 = 0.519803;\ a = 2.04082\)
\(a = 2.04082,\ b = 1\) のときの曲率円の半径 = 0.489998
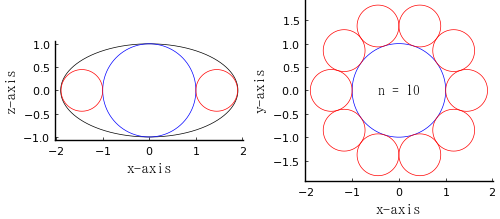
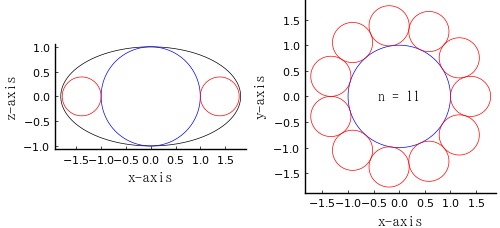
\(n = 10, 11, \dots\) のときは,萠黄球の半径が曲率円の半径より小さくなり,「楕円と 2 点で接する」という条件を満たさない。
\(r_1 = b = 1;\ n = 10;\ r_2 = 0.447214;\ a = 1.90211\)
\(a = 1.90211,\ b = 1\) のときの曲率円の半径 = 0.525731
\(r_1 = b = 1;\ n = 11;\ r_2 = 0.392239;\ a = 1.81405\)
\(a = 1.81405,\ b = 1\) のときの曲率円の半径 = 0.551254
:
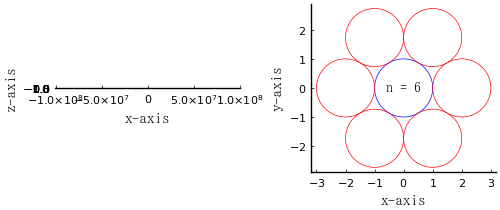
描画関数プログラムのソースを見る
function draw(b, n, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = b
r2 = -b*sin(pi/n)/(sin(pi/n) - 1)
a = sqrt(2)*b^(3/2)*sqrt(1/(b - r2))
(r2, a) = (-b*sin(pi/n)/(sin(pi/n) - 1), sqrt(2)*b*sqrt( (sin(pi/n) - 1)/(2*sin(pi/n) - 1)))
r0 = b^2/a
@printf("r1 = b = %g; n = %d; r2 = %.15g; a = %.15g\n", r1, n, r2, a)
@printf("a = %g, b = %g のときの曲率円の半径 = %g\n", a, b, r0)
p1 = plot(xlabel="x-axis", ylabel="z-axis")
ellipse(0, 0, a, b, color=:black)
circle(0, 0, r1, :blue)
circle2(r1 + r2, 0, r2)
p2 = plot(xlabel="x-axis", ylabel="y-axis")
circle(0, 0, r1, :blue)
rotate(r1 + r2, 0, r2, angle=360/n)
point(0, 0, @sprintf("n = %d", n), :black, :center, :vcenter, mark=false)
plot(p1, p2)
end;
draw(1, 6, true)
以下のアイコンをクリックして応援してください