算額（その1725） - 算額あれこれ

香川県丸亀市天満町天満天神社（天満宮）明治33年(1900)

本田益夫：算額随想-香川県内の算額について-，私家版（香川県立図書館蔵），昭和45年(1970).
キーワード：円3個，正三角形
#Julia #SymPy #算額 #和算 #数学

正三角形の中に 3 個の等円を容れる。黒積（正三角形の面積から，等円 3 個の面積を除いた面積）が 293.432182 寸（歩）のとき，三角面（正三角形の一辺の長さ）はいかほどか。

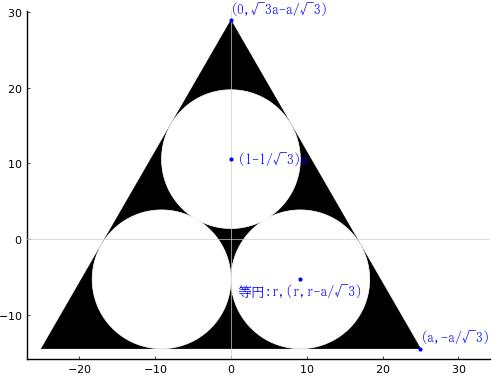
黒積を \(S\)，正三角形の一辺の長さを \(2a\)，等円の半径を \(r\) として，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms a::positive, r::positive, S::positive
eq1 = r/(a - r) - 1/√Sym(3)
eq2 = 2a*√Sym(3)a/2 - 3*PI*r^2 - S;

res = solve([eq1, eq2], (a, r))[1]

(sqrt(S)*(1 + sqrt(3))/sqrt(-3*pi + 6 + 4*sqrt(3)), sqrt(S)/sqrt(-3*pi + 6 + 4*sqrt(3)))

# a
res[1] |> display
res[1] |> println

\( \displaystyle　\frac{\sqrt{S} \left(1 + \sqrt{3}\right)}{\sqrt{- 3 \pi + 6 + 4 \sqrt{3}}}\)

sqrt(S)*(1 + sqrt(3))/sqrt(-3*pi + 6 + 4*sqrt(3))

# 2a 正三角形の一辺の長さ
res[1](S => 293.432182).evalf() * 2 |> println

50.0064713066296

# r
res[2] |> display
res[2] |> println
res[2](S => 293.432182).evalf() |> println

\( \displaystyle　\frac{\sqrt{S}}{\sqrt{- 3 \pi + 6 + 4 \sqrt{3}}}\)

sqrt(S)/sqrt(-3*pi + 6 + 4*sqrt(3))
9.15181942592202

なお，eq1 より，\(r = a(\sqrt{3} - 1)/2\) でもある。

描画関数プログラムのソースを見る

function draw(S, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
t = sqrt(6 + 4√3 - 3pi)
(a, r) = (√S*(1 + √3)/t, √S/t)
plot([a, 0, -a, a], [-a/√3, √3a - a/√3, -a/√3, -a/√3], seriestype=:shape, fillcolor=:black, lw=0.5)
rotatef(r, r - a/√3, r, :white)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) / 3 # size[2] * fontsize * 2
vline!([0], color=:gray80, lw=0.5)
hline!([0], color=:gray80, lw=0.5)
point(a, -a/√3, "(a,-a/√3)", :blue, :left, :bottom, delta=delta)
point(0, √3a - a/√3, "(0,√3a-a/√3)", :blue, :left, :bottom, delta=delta)
point(r, r - a/√3, "等円:r,(r,r-a/√3)", :blue, :center, delta=-delta)
point(0, (1 - 1/√3)a, " (1-1/√3)a", :blue, :left, :vcenter)
xlims!(-a - 3delta, a + 15delta)
end
end;