算額（その1686） - 算額あれこれ

18 岩手県江刺市大通り中善観音文政10年(1827)

安富有恒：和算—岩手の現存算額のすべて，青磁社，東京都，1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード：円2個，正方形
#Julia #SymPy #算額 #和算 #数学

正方形の中に小さな正方形を 2 個容れ，甲円と乙円を 2 個ずつ容れる。乙円の直径が与えられたとき，甲円の直径はいかほどか。

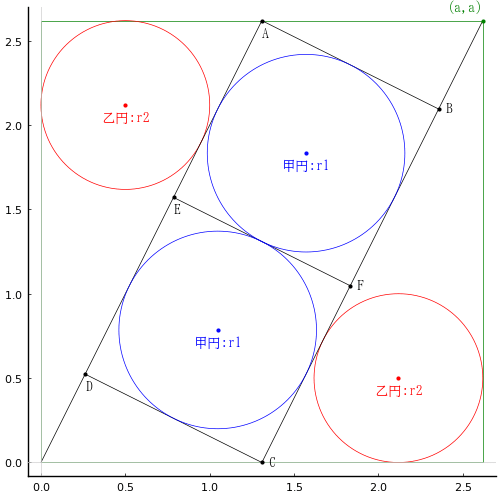
甲円の半径を \(r_1\)
乙円の半径を \(r_2\)
正方形の一辺の長さを \(a\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms a::positive, b::positive, r1::positive,
r2::positive
b = a/2
eq1 = b/a- (sqrt(a^2 + b^2) - 4r1)/2r1
eq2 = a + b - sqrt(a^2 + b^2) - 2r2
res = solve([eq1, eq2], (r1, a))

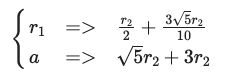
# r1 甲円の半径
res[r1] |> simplify |> println

r2*(5 + 3*sqrt(5))/10

甲円の半径 \(r_1\) は，乙円の半径 \(r_2\) の \( (5 + 3\sqrt{5})/10\) 倍である。
たとえば，乙円の直径が 1 寸のとき，甲円の直径は \( (5 + 3\sqrt{5})/10 = 1.170820393249937\) 寸である。

術は以下のようになっており，上記の解と一致している。

@syms 乙円径
甲円径 = (sqrt(1.8) + 1)*乙円径/2
甲円径(乙円径 => 1) |> println

1.17082039324994

# a 正方形の一辺の長さ
res[a] |> simplify |> println

r2*(sqrt(5) + 3)

正方形の一辺の長さ a は，乙円の半径の \( (\sqrt{5} + 3)\) 倍である。
たとえば，乙円の直径が 1 寸のとき，正方形の一辺の長さは \( (\sqrt{5} + 3)\cdot (1/2) = 2.618033988749895\) 寸である。

描画関数プログラムのソースを見る

function draw(r2, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = r2*(5 + 3√5)/10
a = r2*(√5 + 3)
b = a/2
@printf("乙円の直径が %g のとき，甲円の直径は %g である。なお，正方形の一辺の長さは %g である。\n", 2r2, 2r1, a)
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
circle(r2, a - r2, r2)
circle(a - r2, r2, r2)
θ = atand(2)
(Ax, Ay) = (b, a)
(Bx, By) = (b + 2r1*sind(θ), a - 2r1*cosd(θ))
(Cx, Cy) = (b, 0)
(Dx, Dy) = (b - 2r1*sind(θ), 2r1*cosd(θ))
(Ex, Ey) = ( (2b - 2r1*sind(θ))/2, (a + 2r1*cosd(θ))/2)
(Fx, Fy) = ( (2b + 2r1*sind(θ))/2, (a - 2r1*cosd(θ))/2)
segment(0, 0, Ax, Ay)
segment(Cx, Cy, a, a)
segment(Ax, Ay, Bx, By)
segment(Ex, Ey, Fx, Fy)
segment(Cx, Cy, Dx, Dy)
(o1x, o1y) = ( (Ax + Fx)/2, (Ay + Fy)/2)
circle(o1x, o1y, r1, :blue)
(o2x, o2y) = ( (Ex + Cx)/2, (Ey + Cy)/2)
circle(o2x, o2y, r1, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(Ax, Ay, "A", :black, :left, delta=-delta)
point(Bx, By, " B", :black, :left, :vcenter)
point(Cx, Cy, " C", :black, :left, :vcenter)
point(Dx, Dy, "D", :black, :left, delta=-delta)
point(Ex, Ey, "E", :black, :left, delta=-delta)
point(Fx, Fy, " F", :black, :left, :vcenter)
point(o1x, o1y, "甲円:r1", :blue, :center, delta=-delta)
point(o2x, o2y, "甲円:r1", :blue, :center, delta=-delta)
point(r2, a - r2, "乙円:r2", :red, :center, delta=-delta)
point(a-r2, r2, "乙円:r2", :red, :center, delta=-delta)
point(a, a, "(a,a)", :green, :right, :bottom, delta=delta)
end
end;