44 岩手県一関市滝沢字寺田下 熊野白山滝神社 明治31年(1898)
安富有恒:和算—岩手の現存算額のすべて,青磁社,東京都,1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード:3次元,球,円錐
#Julia #SymPy #算額 #和算 #数学
盤上に 5 個の円錐が底面の中心が円周上にあり底面で互いに外接している。その中心に1個の球を容れる。球は盤面に接し,またそれぞれの円錐と 1 点で外接している。球の高さと円錐の高さは等しい。円錐の底面の直径が与えられたとき,球の直径はいかほどか。
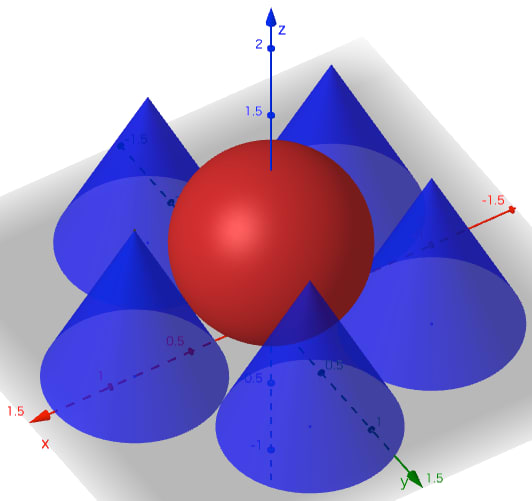
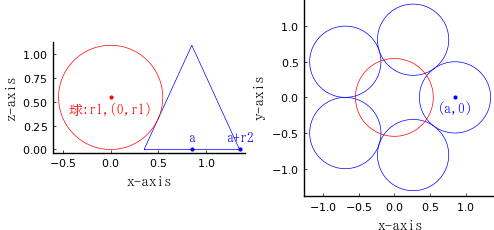
球の半径と中心座標を \(r_1,\ (0,\ 0,\ r_1)\)
円錐の底面の半径と中心座標を \(r_2,\ (a\cos\theta,\ a\sin\theta);\ \theta = 0°, 72°, 144°, 216°, 288°\)
とおき,以下の連立方程式を解く。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a::positive, r1::positive, r2::positive
eq1 = dist2(a - r2, 0, a, 2r1, 0, r1, r1)
eq2 = a*sind(Sym(36)) - r2
res = solve([eq1, eq2], (r1, a))[1]
(sqrt(-2*sqrt(2)*r2^2*sqrt(5 - sqrt(5)) + 8*r2^2)/sqrt(5 - sqrt(5)), 2*sqrt(2)*r2/sqrt(5 - sqrt(5)))
# r1
res[1] |> simplify
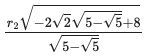
円錐の底面の半径 \(r_2\) が 1/2 のとき,球の半径 \(r_1\) は 0.546151438315381 である。
res[1](r2 => 1/2).evalf() |> println
0.546151438315381
術は以下の通りで,上の解と一致する。
円錐径 = 1
天 = sqrt(0.8) + 2
球径 = sqrt(天 - sqrt(天))*円錐径
1.0923028766307612
描画関数プログラムのソースを見る
function draw(r2)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, a) = (sqrt(-2*sqrt(2)*r2^2*sqrt(5 - sqrt(5)) + 8*r2^2)/sqrt(5 - sqrt(5)), 2*sqrt(2)*r2/sqrt(5 - sqrt(5)))
@printf("円錐の底面の直径が %g のとき,球の直径は %g である。\n", 2r2, 2r1)
p1 = plot([a - r2, a + r2, a, a - r2], [0, 0, 2r1, 0], color=:blue, lw=0.5, xlabel="x-axis", ylabel="z-axis")
circle(0, r1, r1)
p2 = plot(xlabel="x-axis", ylabel="y-axis")
rotate(a, 0, r2, :blue, angle=72)
circle(0, 0, r1)
plot(p1, p2)
end;
draw(1/2)
以下のアイコンをクリックして応援してください