続神壁算法 10 東都愛宕山 文化2年(1805)
南筑米藩 藤田貞資門人 上州沼田藩 堀田文兵衛光長
キーワード:3次元,球,円錐
#Julia #SymPy #算額 #和算 #数学
円錐の中に,大球を 1 個,小球を複数個容れる。小球は円錐の側面と底面の二箇所で接し,大球,隣の小球と接している。円錐の高さと底面の円の直径が与えられたとき,小球の個数を求める術を述べよ。
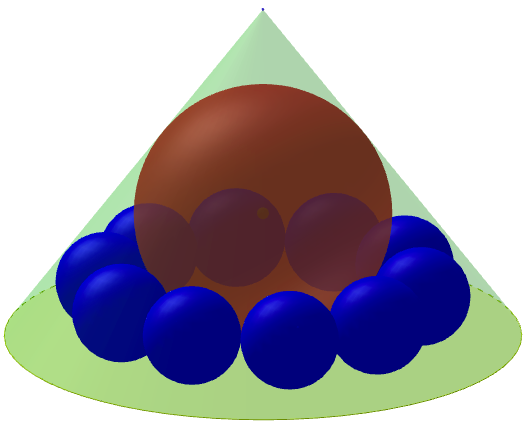
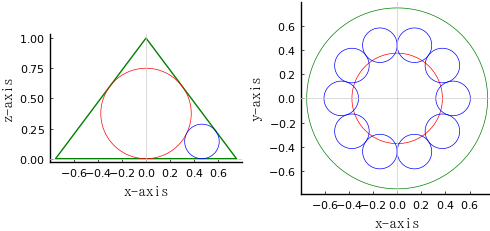
円錐の高さと底面の半径を \(a,\ h\)
大球の半径と中心座標を \(r_1,\ (r_1,\ 0)\)
小球の個数,半径と中心座標を \(n,\ r_2,\ (2\sqrt{r_1\ r_2},\ r_2)\)
小球の中心は半径 \(2\sqrt{r_1\ r_2}\) の円周上にある。
隣り合う 2 個の小球の中心と円の中心との間の角度を \(180/n\)
とおき,以下の連立方程式を解く。
「問」では単に,「円錐の高さと底面の円の直径が与えられたとき」とあるが,どんな値でも与えて良いものではない。条件を満たさない数値が与えられると,小球の個数は整数値でなくなる。すなわち,その整数部をとった個数なら小球の間には隙間ができるし,整数部 + 1 の個数なら,はみ出す(入らない)。
条件式は以下の 3 個で,変数は 5 個である。すなわち,変数のうちのどれか 2 つが定数として決まらないと連立方程式は解けない。
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a::positive, h::positive, r1::positive,
r2::positive, n::positive
eq1 = r1/a - r2/(a - 2sqrt(r1*r2))
eq2 = a/sqrt(a^2 + h^2) - r1/(h - r1)
eq3 = 2sqrt(r1*r2)*sind(Sym(180)/n) - r2
\(\displaystyle 2 \sqrt{r_{1}} \sqrt{r_{2}} \sin{\left(\frac{\pi}{n} \right)} - r_{2}\)
まず最初に,小球の個数 \(n\) と円錐の高さ \(h\) が与えられたとき,円錐の底面の半径 \(a\),大球の半径 \(r_1\),小球の半径 \(r_2\) を求める場合について検討する。
res1 = solve([eq1, eq2, eq3], (a, r1, r2))[1]
(h*(-4*cos(2*pi/n) - 2*cos(4*pi/n) + 5)/(8*(2*cos(2*pi/n) - 1)*Abs(sin(pi/n))), h*(4*cos(2*pi/n) + 2*cos(4*pi/n) - 5)/(-sqrt(1/( (2*cos(2*pi/n) - 1)^2*sin(pi/n)^2))*(2*cos(2*pi/n) - 3)^2*(2*cos(2*pi/n) - 1)*Abs(sin(pi/n)) + 4*cos(2*pi/n) + 2*cos(4*pi/n) - 5), 4*h*(4*cos(2*pi/n) + 2*cos(4*pi/n) - 5)*sin(pi/n)^2/(-sqrt(1/( (2*cos(2*pi/n) - 1)^2*sin(pi/n)^2))*(2*cos(2*pi/n) - 3)^2*(2*cos(2*pi/n) - 1)*Abs(sin(pi/n)) + 4*cos(2*pi/n) + 2*cos(4*pi/n) - 5))
「\(n,\ h\) を与えて,\(a,\ r_1,\ r_2\) を得る」関数は以下のようになる。
Abs = abs
# n, h を与えて,a, r1, r2 を得る
get_a_r1_r2(n, h) = (h*(-4*cos(2*pi/n) - 2*cos(4*pi/n) + 5)/(8*(2*cos(2*pi/n) - 1)*Abs(sin(pi/n))), h*(4*cos(2*pi/n) + 2*cos(4*pi/n) - 5)/(-sqrt(1/( (2*cos(2*pi/n) - 1)^2*sin(pi/n)^2))*(2*cos(2*pi/n) - 3)^2*(2*cos(2*pi/n) - 1)*Abs(sin(pi/n)) + 4*cos(2*pi/n) + 2*cos(4*pi/n) - 5), 4*h*(4*cos(2*pi/n) + 2*cos(4*pi/n) - 5)*sin(pi/n)^2/(-sqrt(1/( (2*cos(2*pi/n) - 1)^2*sin(pi/n)^2))*(2*cos(2*pi/n) - 3)^2*(2*cos(2*pi/n) - 1)*Abs(sin(pi/n)) + 4*cos(2*pi/n) + 2*cos(4*pi/n) - 5));
たとえば,\(n = 10, h = 1\) のとき,\(a = 0.75\) である。
get_a_r1_r2(10, 1)
(0.7499999999999999, 0.375, 0.1432372542187894)
次に,円錐の底面の半径 \(a\) と円錐の高さ \(h\) が与えられたとき,小球の個数 \(n\),大球の半径 \(r_1\),小球の半径 \(r_2\) を求める場合について検討する。
res2 = solve([eq1, eq2, eq3], (n, r1, r2))[3]
(pi/asin(sqrt(4*a^3 + 4*a^2*sqrt(a^2 + h^2) + 5*a*h^2 - 2*sqrt(2)*a*h*sqrt(a^2 + a*sqrt(a^2 + h^2) + h^2) + 3*h^2*sqrt(a^2 + h^2) - 2*sqrt(2)*h*sqrt(a^2 + h^2)*sqrt(a^2 + a*sqrt(a^2 + h^2) + h^2))/(2*sqrt(4*a^3 + 4*a^2*sqrt(a^2 + h^2) + 3*a*h^2 + h^2*sqrt(a^2 + h^2)))), a*h/(a + sqrt(a^2 + h^2)), a*h*(2*a^2 + 2*a*sqrt(a^2 + h^2) + 3*h^2 - 2*sqrt(2)*h*sqrt(a^2 + a*sqrt(a^2 + h^2) + h^2))/(4*a^3 + 4*a^2*sqrt(a^2 + h^2) + 3*a*h^2 + h^2*sqrt(a^2 + h^2)))
「\(a,\ h\) を与えて,\(n,\ r_1,\ r_2\) を得る」関数は以下のようになる。
# a, h を与えて,n, r1, r2 を得る
get_n_r1_r2(a, h) = (pi/asin(sqrt(4*a^3 + 4*a^2*sqrt(a^2 + h^2) + 5*a*h^2 - 2*sqrt(2)*a*h*sqrt(a^2 + a*sqrt(a^2 + h^2) + h^2) + 3*h^2*sqrt(a^2 + h^2) - 2*sqrt(2)*h*sqrt(a^2 + h^2)*sqrt(a^2 + a*sqrt(a^2 + h^2) + h^2))/(2*sqrt(4*a^3 + 4*a^2*sqrt(a^2 + h^2) + 3*a*h^2 + h^2*sqrt(a^2 + h^2)))), a*h/(a + sqrt(a^2 + h^2)), a*h*(2*a^2 + 2*a*sqrt(a^2 + h^2) + 3*h^2 - 2*sqrt(2)*h*sqrt(a^2 + a*sqrt(a^2 + h^2) + h^2))/(4*a^3 + 4*a^2*sqrt(a^2 + h^2) + 3*a*h^2 + h^2*sqrt(a^2 + h^2)));
get_a_r1_r2(10, 1) において,\(n = 10,\ h = 1\) のとき,\(a = 0.75\) であった。
get_n_r1_r2(a, h) により,\(n = 10\) になることが確認できる。
get_n_r1_r2(0.75, 1)
(10.0, 0.375, 0.1432372542187894)
その他の例は,以下のようになる。
# n = 6 の場合
get_a_r1_r2(6, 1) |> println
get_n_r1_r2(4.5035996273704955e15, 1) |> println
(4.5035996273704955e15, 0.5, 0.4999999999999999)
(6.0, 0.5, 0.4999999999999999)
# n = 7 の場合
get_a_r1_r2(7, 1) |> println
get_n_r1_r2(3.442365049988173, 1) |> println
(3.442365049988173, 0.48987429076397315, 0.36888533255971184)
(7.0, 0.48987429076397315, 0.36888533255971173)
# n = 15 の場合
get_a_r1_r2(15, 1) |> println
get_n_r1_r2(0.005493192097621909, 1) |> println
(0.005493192097621909, 0.0054630998165489586, 0.0009446195889850623)
(15.000000000000016, 0.005463099816548959, 0.0009446195889850597)
以上のように,\(a,\ h\) は特定の場合でなければ小球の個数 \(n\) は整数にならない。
正しい \(a,\ h\) が与えられた場合,小球の個数は以下により計算される。
ans_n = pi/asin(sqrt(4*a^3 + 4*a^2*sqrt(a^2 + h^2) + 5*a*h^2 - 2*sqrt(Sym(2))*a*h*sqrt(a^2 + a*sqrt(a^2 + h^2) + h^2) + 3*h^2*sqrt(a^2 + h^2) - 2*sqrt(Sym(2))*h*sqrt(a^2 + h^2)*sqrt(a^2 + a*sqrt(a^2 + h^2) + h^2))/(2*sqrt(4*a^3 + 4*a^2*sqrt(a^2 + h^2) + 3*a*h^2 + h^2*sqrt(a^2 + h^2))))
\(\displaystyle \frac{\pi}{\operatorname{asin}{\left(\frac{\sqrt{4 a^{3} + 4 a^{2} \sqrt{a^{2} + h^{2}} + 5 a h^{2} - 2 \sqrt{2} a h \sqrt{a^{2} + a \sqrt{a^{2} + h^{2}} + h^{2}} + 3 h^{2} \sqrt{a^{2} + h^{2}} - 2 \sqrt{2} h \sqrt{a^{2} + h^{2}} \sqrt{a^{2} + a \sqrt{a^{2} + h^{2}} + h^{2}}}}{2 \sqrt{4 a^{3} + 4 a^{2} \sqrt{a^{2} + h^{2}} + 3 a h^{2} + h^{2} \sqrt{a^{2} + h^{2}}}} \right)}}\)
上に示した \(a = 0.75,\ h = 1\) の場合は,正しく \(n = 10\) となる。
ans_n(a => 0.75, h => 1).evalf() |> println
10.0000000000000
いい加減な数値を指定すると,小球の個数は整数にならない。
ans_n(a => 0.7, h => 1).evalf() |> println
10.1919797821797
描画関数プログラムのソースを見る
function draw(a, h, more=true)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
Abs = abs
(n, r1, r2) = get_n_r1_r2(a, h)
@printf("a = %.15g; h = %.15g; n = %g; r1 = %.15g; r2 = %.15g\n", a, h, n, r1, r2)
p1 = plot([-a, a, 0, -a], [0, 0, h, 0], color=:green, xlabel="x-axis", ylabel="z-axis")
circle(0, r1, r1)
circle(2sqrt(r1*r2), r2, r2, :blue)
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
p2 = plot(xlabel="x-axis", ylabel="y-axis")
circle(0, 0, r1)
circle(0, 0, a, :green)
rotate(2sqrt(r1*r2), 0, r2, :blue, angle=360/n)
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
plot(p1, p2)
end;
draw(0.75, 1, true)
以下のアイコンをクリックして応援してください