大阪住吉神社 弘化3年(1846)
福田理軒:順天堂算譜,明治6年(1873)
深川英俊,トニー・ロスマン:聖なる数学:算額,森北出版株式会社,2010年4月22日.
福島県郡山市中田町上石 国見山稲荷 明治11年(1878)
五輪教一:黄金比の眠るほこら,日本評論社,2015年7月10日
キーワード:正方形
#Julia #SymPy #算額 #和算 #数学
図のように,直線 l 上に一辺の長さが \(a\) の正方形 ABCD が固定されている。同じ大きさの動く正方形 EFGH が直線(上に載っていて,辺 CD に接してながら回転していて,l 上の接点をE,CD 上の接点を F とする。頂点 H を通り l に垂直な動く直線と l との交点を P,2点 B,G を通る直線との交点を T とする。PT の最大値を a で表せ。
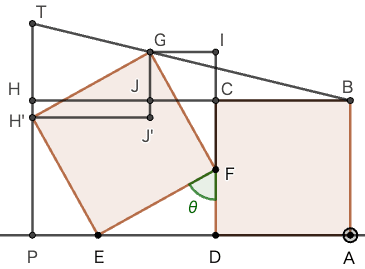
TP = TH + a
TH/BH = GJ/BJ --> TH = BH*GJ/BJ
BH = a*sin(θ) + a*cos(θ) + a
GJ = FI + DF - a = a*sin(θ) + a*cos(θ) - a
BJ = GI + a = a*cos(θ) + a
TP = (a*sin(θ) + a*cos(θ) + a)*(a*sin(θ) + a*cos(θ) - a)/(a*cos(θ) + a) + a
include("julia-source.txt"); # julia-source.txt ソース
using SymPy
@syms a::positive, θ::positive
TP = (a*sin(θ) + a*cos(θ) + a)*(a*sin(θ) + a*cos(θ) - a)/(a*cos(θ) + a) + a;
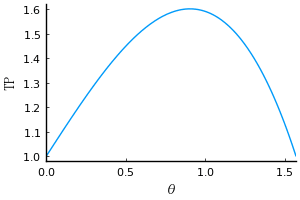
TP は \(\theta\) の関数で,\(\theta = 1\) のあたりで最大値を取ることがわかる。
pyplot(size=(300, 200), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(TP(a => 1), xlims=(0, pi/2), xlabel="θ", ylabel="TP")
# 導関数を求める
g = diff(TP, θ);
# 導関数 = 0 となるときの θ を求める
ans_θ = solve(g, θ)[1]
ans_θ |> println
2*atan(sqrt(-2 + sqrt(5)))
# 最大値を求める
TP(θ => ans_θ) |> simplify |> factor
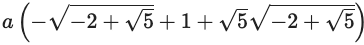
SymPy ではこれ以上簡約化されないが,手計算により以下のようになる。
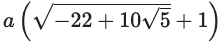
以下のアイコンをクリックして応援してください