算額（その1496） - 算額あれこれ

28 岩手県一関市萩荘字八幡八幡神社弘化3年(1846)

安富有恒：和算—岩手の現存算額のすべて，青磁社，東京都，1987.
http://www.wasan.jp/iwatenosangaku_yasutomi.pdf
キーワード：円数個，包絡線
#Julia #SymPy #算額 #和算 #数学

複数の円が互いに外接している（内部には空隙がある）。円の個数が与えられたとき円の包絡線の周長を求める術を述べよ。

幾何学的に正確に述べれば，正 \(n\) 角形の頂点を中心とする，半径が正 \(n\) 角形の一辺の長さの 1/2 の円を \(n\) 個描く。隣り合う 2 つの円の共通接線の接点間の距離と一つの円の接点間の短い方の円弧の長さの和を求める術を述べよ（かえってわかりにくくなった）。

要するに，以下のような図で，緑の円弧の長さと青の線分の長さの和を求めよということ。

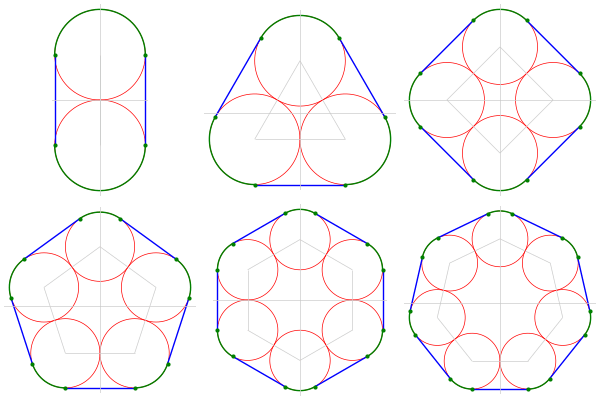
よく観察すればわかるが，円の直径を \(d\) とすれば，緑の円弧の長さの和は \(n\) にかかわらず \(\pi d\)，青の線分の長さの和は \(n d\) である。青の線分は，円の中心を結ぶ正 \(n\) 角形の辺であることもわかる。両者の和は \(d(\pi + n)\) である。術にある通り，「円の個数と円周率を加え円の直径を掛ける」となる。

描画関数プログラムのソースを見る

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms n, R, r
eq = (R - r)*sind(180/n) - r
res = solve(eq, R)[1];

# 半径 r の円の中心が円周上にある円の半径 R
res |> println

r + r/sin(pi/n)

function draw(n, more=false)
pyplot(size=(600, 400), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 1/2
θ =360/n
θ2 = (0:n).*θ .+ 90
R = r + r/sind(θ/2)
x = (R - r).*cosd.(θ2)
y = (R - r).*sind.(θ2)
p = plot(showaxis=false)
rotate(0, R - r, r, angle=θ, lw=0.1)
for i = 1:n
segment(x[i], y[i], x[i + 1], y[i + 1], :gray80, lw=0.5)
θ3 = (i - 1)*θ + 90 + θ/2
x1 = x[i] + r*cosd(θ3)
y1 = y[i] + r*sind(θ3)
x2 = x[i + 1] + r*cosd(θ3)
y2 = y[i + 1] + r*sind(θ3)
segment(x1, y1, x2, y2, :blue, lw=1)
circle(x[i], y[i], r, beginangle=θ3 - θ, endangle=θ3, :green, lw=1)
point(x1, y1)
point(x2, y2)
end
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
end
return p
end;