算額（その734） - 算額あれこれ

福島県田村市安倍文殊菩薩堂明治10年(1877)

深川英俊，トニー・ロスマン：聖なる数学：算額，p. 100，森北出版株式会社，2010年４月22日.

福島県安達郡東和町木幡山（現二本松市）隠津島神社明治17年(1884)

～落書き帳「○△□」～ 16．また一寸（○△□のおにぎり弁当）
http://streetwasan.web.fc2.com/math15.5.23.html

キーワード：円1個，正方形，正三角形，直角三角形
#Julia #SymPy #算額 #和算 #数学

直角三角形の中に，正方形，円，正三角形が互いに接して入っている。鈎の長さが 1 寸のとき，「子」の長さはいかほどか。

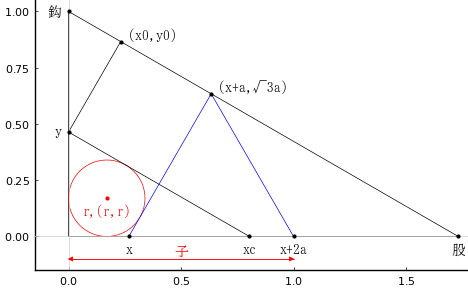
「\(鈎\)」，「\(股\)」，「\(弦\)」をそのまま変数名として使う。
正三角形の一辺の長さを \(a\)，正方形の一辺の長さを \(b\)，円の半径を \(r\) として以下の方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
r::positive, a::positive, b::positive,
xc::positive, x::positive, y::positive,
x0::positive, y0::positive, d
弦 = sqrt(鈎^2 + 股^2)
eq1 = 股*y - xc*鈎
eq2 = sqrt(Sym(3))a/(股 - (x + a)) - 鈎/股
eq2 = sqrt(Sym(3))a*股 - 鈎*(股 - (x + a))
eq3 = b*弦 - 股*(鈎 - y)
eq4 = dist(x, 0, x + a, sqrt(Sym(3))a, r, r) - r^2
eq4 = numerator(apart(eq4, d))
eq5 = sqrt( (鈎 - y)^2 - b^2) + b + sqrt(3a^2 + (股 - x - a)^2) - 弦
eq6 = y + xc - sqrt(y^2 + xc^2) - 2r
eq7 = dist(x, 0, x + a, sqrt(Sym(3))a, 0, y) - b^2
eq7 = numerator(apart(eq7, d))
eq8 = x0^2 + (y0 - y)^2 - b^2
eq9 = (鈎 - y0)/x0 - 鈎/股;

function H(u)
(股, r, a, b, x, y, xc, x0, y0) = u
return [
-xc + y*股, # eq1
sqrt(3)*a*股 + a + x - 股, # eq2
b*sqrt(股^2 + 1) - 股*(1 - y), # eq3
-sqrt(3)*r^2/2 - 3*r*x/2 + sqrt(3)*r*x/2 + 3*x^2/4, # eq4
b + sqrt(3*a^2 + (-a - x + 股)^2) + sqrt(-b^2 + (1 - y)^2) - sqrt(股^2 + 1), # eq5
-2*r + xc + y - sqrt(xc^2 + y^2), # eq6
-b^2 + 3*x^2/4 + sqrt(3)*x*y/2 + y^2/4, # eq7
-b^2 + x0^2 + (-y + y0)^2, # eq8
-1/股 + (1 - y0)/x0, # eq9
]
end;

鈎 = 1
iniv = BigFloat[1.7, 0.17, 0.37, 0.5, 0.27, 0.46, 0.8, 0.23, 0.87]
res = nls(H, ini=iniv)

([1.7320508075688772, 0.16987298107780677, 0.36602540378443865, 0.4641016151377546, 0.2679491924311227, 0.4641016151377546, 0.8038475772933681, 0.2320508075688773, 0.8660254037844386], true)

直角三角形は辺の比が \(2:1:\sqrt{3}\) のよく見かけるものだ。

鈎が 1 寸のとき，「子」も 1 寸である。

その他のパラメータは，以下のとおりである。

\(子 = 1.0;\ 弦 = 1.9999999999999998;\ b = 0.4641016151377546\)
\(股 = 1.73205;\ r = 0.169873;\ a = 0.366025;\ b = 0.464102\)
\(x = 0.267949;\ y = 0.464102;\ x_c = 0.803848\)
\(x_0 = 0.232051;\ y_0 = 0.866025\)

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
鈎 = 1
(股, r, a, b, x, y, xc, x0, y0) = res[1]
弦 = sqrt(鈎^2 + 股^2)
@printf("子 = %.15g, 弦 = %.15g, b = %.15g\n", x + 2a, 弦, b)
@printf("股 = %g; r = %g; a = %g; b = %g; x = %g; y = %g; xc = %g; x0 = %g; y0 = %g\n", 股, r, a, b, x, y, xc, x0, y0)
plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:black, lw=0.5)
circle(r, r, r)
segment(x, 0, x + a, √3a, :blue)
segment(x + 2a, 0, x + a, √3a, :blue)
segment(0, y, xc, 0)
segment(0, y, x0, y0)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(r, r, "r,(r,r)", :red, :center, delta=-2delta)
point(x0, y0, " (x0,y0)", :black, :left, :bottom)
point(x + a, √3a, " (x+a,√3a)", :black, :left, :bottom)
point(0, 鈎, "鈎 ", :black, :right, :vcenter)
point(0, y, "y ", :black, :right, :vcenter)
point(股, 0, "股", :black, :center, delta=-2delta)
point(x, 0, "x", :black, :center, delta=-2delta)
point(x + 2a, 0, "x+2a", :black, :center, delta=-2delta)
point(xc, 0, "xc", :black, :center, delta=-2delta)
plot!(xlims=(-0.15, 1.9), ylims=(-0.15, 1.1))
arrow(0, 0, x + 2a, 0, :both)
dimension_line(0.0, -0.1, x + 2a, -0.1, "子", color=:red, horizontal=:center, vertical=:bottom, delta=delta/2)
end
end;