算額（その693） - 算額あれこれ

神壁算法關流藤田貞資門人毛利石見守家士山邊平助清誠寛政七年

藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf
キーワード：外円，長方形
#Julia #SymPy #算額 #和算 #数学

「算額（その602）」に似ている（求めるものが違うが，本質的に同じ）。

外円内に長方形を \(n\) 個容れる。それぞれの長方形の長辺の 2 頂点は外円の円周上にあり，残りの 2 頂点は隣の長方形と共有している。
長方形の長辺が 3 寸のとき，外積が最小（\(n\) 個の面積の和が最大）になるのは，外円の直径がいかほどのときか。

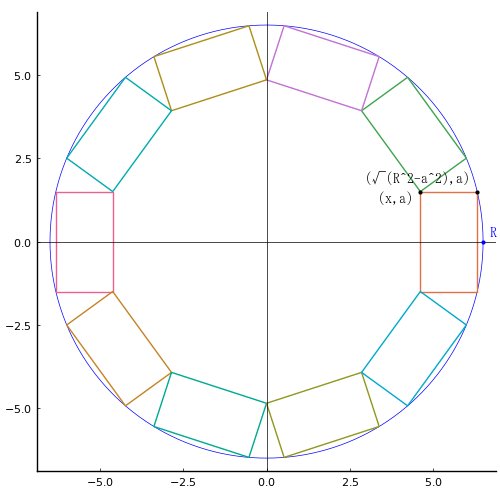
外円の半径を \(R\), 内接する長方形の長辺の長さを \(2a\) とする。
長方形の頂点座標 \( (x,\ a),\ (\sqrt{R^2 - a^2},\ a)\) を求める。
長方形の面積の和は \(n(2a(\sqrt{R^2 - a^2} - x))\) である。
外積は外円の面積から長方形の面積の和を差し引いたものである。これを \(B\) とすれば，\(B = \pi R^2 - n(2a (\sqrt{R^2 - a^2} - x))\) となる。

なお，上の図は「神壁算法」にある図に近いように描いたものであるが，これは外円の直径が 13 寸のときのもので，外積は 81.4913891769524 なので，最小値からはかけ離れている。

実際に外積が最小となる場合の図は下の方に示す。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy
@syms n, a, R, B;

x = a/tand(Sym(180)/n)
B = PI*R^2 - n*2a*(sqrt(R^2 - a^2) - x)
B |> println

pi*R^2 - 2*a*n*(-a/tan(pi/n) + sqrt(R^2 - a^2))

たとえば，問のように \(n = 10,\ a = 3/2\) の場合には，以下の \(B_2\) のようになる。

B2 = B(n => 10, a => 3//2)
B2 |> println

pi*R^2 - 30*sqrt(R^2 - 9/4) + 45/sqrt(1 - 2*sqrt(5)/5)

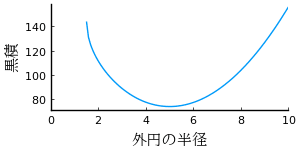
\(B_2\) の値は \(R\) により変化するが，\(R = 5\) 近辺で最小値を取ることがわかる。

using Plots
pyplot(size=(300, 150), grid=false, aspectratio=:none, label="")
plot(B2, xlims=(0,10), xlabel="外円の半径", ylabel="黒積")

\(B\) が最小値となるのは，\(B\) の導関数が 0 になるときである。

まず，導関数 \(g\) を求める。

g = diff(B, R)
g |> println

-2*R*a*n/sqrt(R^2 - a^2) + 2*pi*R

導関数 = 0 となる \(R\) を求めるために solve() を用いる。

R0 = solve(g, R)[3] # 3 of 3
a*sqrt(n^2 + pi^2)/pi

\(a,\ n\) に具体的な値を代入すれば，黒積が最小になるときの外円の半径が得られる。

R0(a=>3/2, n => 10).evalf() |> println

5.00472439995710

外円の半径が与えられると黒積が得られる。

B(R => R0]) |> println

a^2*(n^2 + pi^2)/pi - 2*a*n*(-a/tan(pi/n) + sqrt(a^2*(n^2 + pi^2)/pi^2 - a^2))

\(a,\ n\) に具体的な値を代入すれば，黒積が最小のときの値が得られる。

B(R => R0, a=>3/2, n => 10).evalf() |> println

73.9446182521105

長辺の長さが 3 の 10 個の長方形を入れるとき，外円の直径が 10.0094 のときに黒積が最小値 73.9446 をとる。

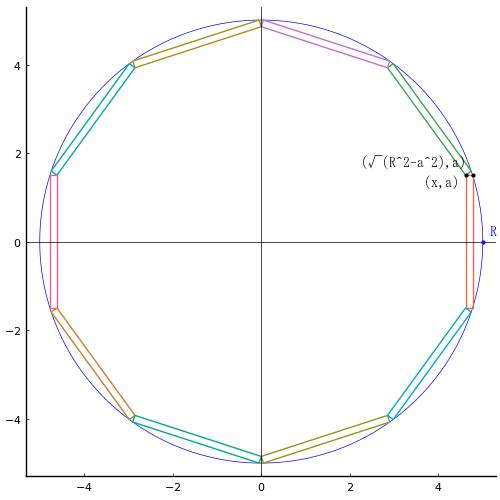
描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(n, a) = (10, 3//2) # 条件として与えられる
x = a/tand(Sym(180)/n)
R = a*sqrt(n^2 + pi^2)/pi
B = a^2*(n^2 + pi^2)/pi - 2*a*n*(-a/tan(pi/n) + sqrt(a^2*(n^2 + pi^2)/pi^2 - a^2))
B0 = pi*R^2 - n*2a*(sqrt(R^2 - a^2) - x)
@printf("長辺の長さが %g の %i 個の長方形を入れるとき，外円の直径が %g のときに黒積が最小値 %g をとる\n", 2a, n, 2R, B)
plot()
circle(0, 0, R, :blue)
XY = [x sqrt(R^2 - a^2) sqrt(R^2 - a^2) x x;
-a -a a a -a]
for deg in 0:360/n:359
XY2 = [cosd(deg) -sind(deg); sind(deg) cosd(deg)] * XY
plot!(XY2[1, :], XY2[2, :])
end
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(R, 0, " R", :blue, :left, :bottom, delta=delta/2)
point(x, a, "(x,a) ", :black, :right, :top)
point(√(R^2-a^2), a, "(√(R^2-a^2),a) ", :black, :right, :bottom, delta=delta)
end
end;