算額（その640） - 算額あれこれ

長野県伊達市羽広仲仙寺文政9年(1826)

中村信弥「改訂増補長野県の算額」県内の算額(P.111)
http://www.wasan.jp/zoho/zoho.html
キーワード：累円，直角三角形
#Julia #SymPy #算額 #和算 #数学

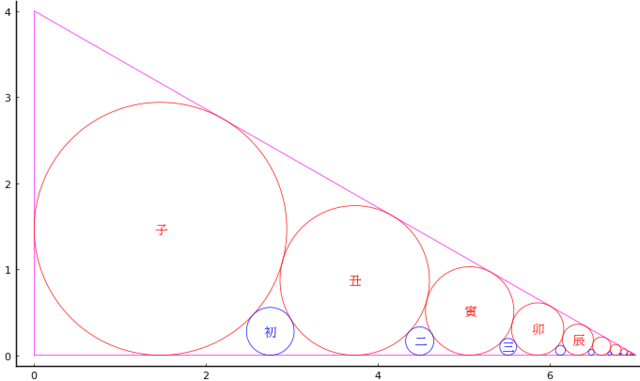
直角三角形内に累円（子円，丑円，寅円,…）が逐次内接し，累円と底辺の隙間に逐円（初円，二円，三円，…，終円）が入っている。初円の直径が 4 寸，終円の直径が 0.5 寸，逐円が 4 個（初円から数えて終円が 4 番目）のときに二円の直径はいかほどか。

子円の半径と中心座標を \(a_0,\ (a_0,\ a_0)\)
丑円の半径と中心座標を \(a_1,\ (xa_1,\ a_1)\)
寅円の半径と中心座標を \(a_2,\ (xa_2,\ a_2)\dots\)
初円の半径と中心座標を \(b_1,\ (xb_1,\ b_1)\)
二円の半径と中心座標を \(b_2,\ (xb_2,\ b_2)\dots\)
とおき，以下の連立方程式により逐次，各円の半径と中心座標を求める。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms 鈎::positive, 股::positive, 弦::positive,
a0::positive
@syms xai::positive, ai::positive, xai1::positive, ai1::positive, bi1::positive, xbi1::positive

function func(ai, xai, 股)
eq1 = (xai1 - xai)^2 + (ai - ai1)^2 - (ai + ai1)^2
eq2 = (xbi1 - xai)^2 + (ai - bi1)^2 - (ai + bi1)^2
eq3 = (xai1 - xbi1)^2 + (ai1 - bi1)^2 - (ai1 + bi1)^2
eq4 = ai/(股 - xai) - ai1/(股 - xai1)
return solve([eq1, eq2, eq3, eq4], (ai1, xai1, bi1, xbi1))
end

(鈎, 股) = (3, 6)
弦 = sqrt(鈎^2 + 股^2)
a0 = (鈎 + 股 - 弦)/2
@printf("弦 =%.15g; a0 = %.15g\n", 弦, a0)

弦 = 6.708203932499369; a0 = 1.1458980337503153

a = Vector{Float64}(undef, 10)
xa = Vector{Float64}(undef, 10)
b = Vector{Float64}(undef, 10)
xb = Vector{Float64}(undef, 10);

(a[1], xa[1], b[1], xb[1]) = func(a0, a0, 股)[1]
for i in 2:10
(a[i], xa[i], b[i], xb[i]) = func(a[i - 1], xa[i - 1], 股)[1]
end

逐円の半径（直径）は初項 \(b[1]\)，公比 \(b[2]/b[1]\) の等比数列である（各項の対数を取るとすぐわかる）。
\(n\) 番目の逐円の半径は \(\displaystyle b[1] \left( \frac{b[2]}{b[1]}\right)^{n-1}\) である。

逆に，\(n\) 番目の逐円の半径がわかっているが公比がわかっていない場合に，公比 \(c\) は以下のようにして求めることができる。
逐円の個数を \(n\)，初円径を \(b_1\)，終円径を \(b_n\) とする。

@syms b1, bn, n, c
res = solve(b1*c^(n - 1) - bn, c)[1] |> println

(bn/b1)^(1/(n - 1))

二円の半径は \(b_1\displaystyle \left(\frac{b_n}{b_1}\right)^{\frac{1}{n - 1}}\) である。

逐円の個数が \(n = 4\)，初円径が \(b_1 = 4\), 終円径が \(b_n = 0.5\) とすると，公比は 0.5 で，二円の径は 2 である。

n = 4
b1 = 4
bn = 0.5
c = (bn/b1)^(1/(n - 1))
(c, b1*c)

(0.5, 2.0)