算額（その630） - 算額あれこれ

和算図形問題あれこれ

令和4年8月の問題-No.1
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html
キーワード：円3個，正三角形，斜線
#Julia #SymPy #算額 #和算 #数学

正三角形内に斜線を 3 本引き，分割された領域に直径が 1174 寸の等円を 3 個入れる。正三角形の一辺の長さを求めよ。

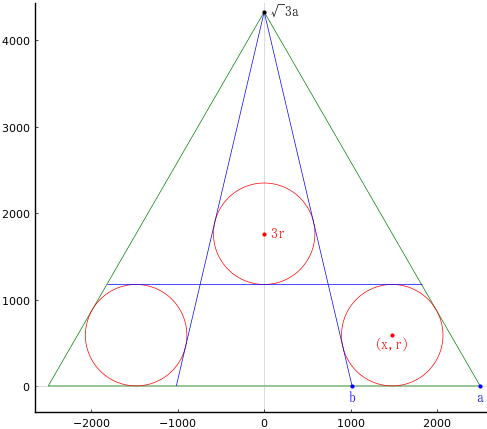
正三角形の一辺の長さを \(2a\)
等円の半径と中心座標を \(r,\ (x,\ r),\ (0,\ 3r)\)
とおき，以下の連立方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms a::positive, b::positive, x::positive, r::positive

r = 1174//2
eq1 = r/(a - x) - 1/sqrt(Sym(3))
三角形の相似から x を求める
r2 = sqrt(Sym(3))a - 2r # 三角形の頂点から真ん中の等円の下端までの距離
r3 = sqrt(Sym(3))a - 3r # 三角形の頂点から真ん中の等円の中心までの距離
eq2 = 2r*r2/sqrt(r3^2 - r^2) - x
eq3 = r/r3 - b/sqrt(3a^2 + b^2);
res = solve([eq1, eq2, eq3], (a, b, x))[1]

(587*sqrt(11)/2 + 1761*sqrt(3)/2, 587*sqrt(3), 587*sqrt(3)/2 + 587*sqrt(11)/2)

res[1] |> factor |> println

587*(sqrt(11) + 3*sqrt(3))/2

正三角形の一辺の長さは \(2a = (\sqrt{11} + 3\sqrt{3})\cdot 等円直径/2 = 4997.000224067413\) である。

(√11 + 3√3)*1174/2 |> println

4997.000224067413

\(正三角形の一辺の長さ = 4997.000224;\ 等円の直径 = 1174\)
\(a = 2498.5;\ b = 1016.71;\ x = 1481.79\)

描画関数プログラムのソースを見る

function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 1174//2
(a, b, x) = (587*sqrt(11)/2 + 1761*sqrt(3)/2, 587*sqrt(3), 587*sqrt(3)/2 + 587*sqrt(11)/2)
@printf("正三角形の一辺の長さ = %.10g; 等円の直径 = %g; a = %g; b = %g; x = %g\n", 2a, 2r, a, b, x)
plot()
vline!([0], color=:gray80, lw=0.5)
hline!([0], color=:gray80, lw=0.5)
plot!([a, 0, -a, a], [0, √3a, 0, 0], color=:green, lw=0.5)
circle(x, r, r)
circle(0, 3r, r)
c = (√3a - 2r)/√3
segment(0, √3a, b, 0, :blue)
segment(0, √3a, -b, 0, :blue)
segment(-c, 2r, c, 2r, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
point(0, 3r, " 3r", :red, :left, :vcenter)
point(x, r, "(x,r)", :red, :center, delta=-delta/2)
point(0, √3a, " √3a", :black, :left, :vcenter)
point(a, 0, "a", :blue, :center, delta=-delta)
point(b, 0, "b", :blue, :center, delta=-delta)
plot!(ylims=(-300, √3a+100))
end
end;