算額（その197） - 算額あれこれ

長野県下高井郡木島平村穂高一川谷大元神社文化8年(1811)

中村信弥「改訂増補長野県の算額」県内の算額(P.91)
http://www.wasan.jp/zoho/zoho.html

岡山県瀬戸内市長船町土師宮森片山日子神社明治6年(1873)

http://www.wasan.jp/okayama/katayamahiko.html
深川英俊，トニー・ロスマン：聖なる数学：算額，p. 145，森北出版株式会社，2010年４月22日.

キーワード：円4個，外円
#Julia #SymPy #算額 #和算 #数学

問2 大円の中に 3 個の小円が互いに外接して入っている。小円の径が 5 寸のとき，大円の径はいかほどか。

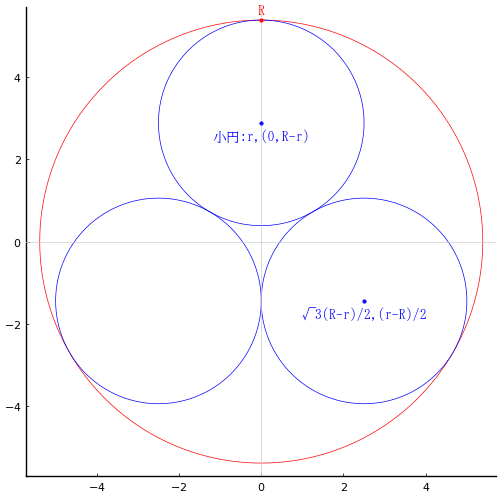
大円の半径と中心座標を \(R,\ (0,\ 0)\)
小円の半径と中心座標を \(r,\ (0,\ R - r),\ ( (R - r)\sqrt{3}/2,\ (r - R)/2)\)
とおき，以下の方程式を解く。

include("julia-source.txt"); # julia-source.txt ソース

using SymPy

@syms R::positive, r::positive;

eq1 = (√Sym(3)*(R - r)/2)^2 + (3(R - r)/2)^2 - (2r)^2
res = solve(eq1, R)[1];

res |> println

r*(3 + 2*sqrt(3))/3

res[R](r => 5).evalf() |> println

10.7735026918963

大円の半径 \(R\) は，小円の半径 \(r\) の \( (3 + 2\sqrt{3})/3\) 倍である。
小円の径が 5 寸のとき，大円の径は 10寸7分7厘3毛5糸である。

算額では 10.77352 寸としているが，末尾桁は 0 または 10.773502 寸有奇の写し間違いであろう。

片山日子神社の算額は，大円の直径から小円の直径を求めるものなので，\(R = r(3 + 2\sqrt{3})/3\) を変換して \(r = R(2\sqrt{3} - 3)\) を得る。

eq = R - r*(3 + 2*√Sym(3))/3
solve(eq, r)[1] |> factor |> println

R*(-3 + 2*sqrt(3))

描画関数プログラムのソースを見る

function draw(r, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = r*(3 + 2√3)/3
@printf("小円の直径が %g のとき，大円の直径は %g である。\n", 2r, 2R)
plot()
circle(0, 0, R)
rotate(0, R - r, r, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R - r, "小円:r,(0,R-r)", :blue, :center, delta=-delta)
point(0, R, "R", :red, :center, :bottom, delta=delta/2)
point(√3(R - r)/2, (r - R)/2, "√3(R-r)/2,(r-R)/2", :blue, :center, delta=-delta)
end
end;